数値解析:帯行列の解法
現在工事中です。 ここでは連立一次方程式の係数行列が帯行列(Band Matrix)となる場合の連立一次方程式の解法について解説する。 化学工学の分野では、典型的には段塔型の蒸留計算はある段(トレイ)の物質収支・熱収支をとるとき、上の段からの液と下の段からの蒸気が流入し、その段上で気液接触を起こし気液平衡となり、その段から上へ蒸気としてまた下へ液として流出する。 これを数式で表し、段に上から順番に番号を割り振り、ある段に着目した物質収支式や熱収支式は、その前後の段にのみ依存し、2段先あるいは算段先以上の段からの項は現れない。 ある変数(たとえば第一成分濃度、温度、気液流量など)を未知数とすると、帯行列を係数行列とする連立方程式で表すことができる。
また反応器解析において基礎式が、微分方程式で表されるとき、これを差分化したときの基礎式も同じく帯行列を係数行列とする連立方程式となる。
蒸留計算や反応器のシミュレーションではいずれも非線形の連立方程式となり、反復して繰り返し計算を行うことになり、帯行列のときの連立一次方程式を解く解法に高速性が必要となる。 ここでは、既存の図書・文献に公表されている帯行列となる連立一次方程式の解法のソースコードを利用し、解を得るまでの計算速度を計測し、比較を行った。
- 1. 帯行列となる連立一次方程式
- 2. バンドマトリックスの解法
- 3. 解法の計算速度比較
- 4. LAPACKのバンドマトリックス解法
- 5. バンドマトリックス解法のまとめ
- 6. Literature Cited
【注】数式表示にはMathJaxを利用しています。IE8以下では表示が遅くなる可能性があります。FireFox などIE8以外のブラウザを利用下さい。
帯行列となる連立一次方程式
帯行列(以下バンドマトリックスと称す)となる連立一次方程式を解く上で必要な基礎的事項について解説する。バンドマトリックスは、対角(Diagonal)要素の上下に帯(バンド)状に非ゼロ要素をもつ行列をいう。 バンド部分以外の要素はすべてゼロである。
一般的に、連立一次方程式の係数行列 \( \bf{A} \) を、正方行列として表示した例を式(1)に示す。 この例では対角要素の上側に1列(NUD=1)、下側に2列(NLD=2)の要素があり、バンド幅はNB=NLD+NUD+1=4の場合を示している。他の対角から離れた要素にはゼロとなる。 FORTRANのコードを効率良く開発する上で、ゼロ要素の多い行列をそのまま正方行列としてメモリ上に配置することはメモリ利用効率面で適切でなく、メモリ効率の良いコンパクトな形式に変換する必要がある。 変換の例を式(2)に示す。列数は\( n \) と変わらないが行数がバンド幅 NB の行列で代替している。全要素数が正方行列のときには \( n^2 \) であったものが、 \( n \) *NB 個の要素に圧縮することができている。
バンドマトリックスの表示例(NLD=2,NLD=1のとき): \[ \begin{align*} \bf{ A } & = \left[\begin{array}{ccccccc} a_{1,1} & a_{1,2} & 0 & 0 & \cdots & 0 & 0 \\ a_{2,1} & a_{2,2} & a_{2,3} & 0 & \cdots & 0 & 0 \\ a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4} & \cdots & 0 & 0 \\ 0 & a_{4,2} & a_{4,3} & a_{4,4} & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & a_{n,n-1} & a_{n,n} \\ \end{array}\right] \tag{1} \\ \\ & = \left[\begin{array}{ccccccc} * & a_{1,2} & a_{2,3} & a_{3,4} & \cdots & \cdots & a_{n-1,n} \\ a_{1,1} & a_{2,2} & a_{3,3} & a_{4,4} & \cdots & \cdots & a_{n,n} \\ a_{2,1} & a_{3,2} & a_{4,3} & a_{5,4} & \cdots & \cdots & * \\ a_{3,1} & a_{4,2} & a_{5,3} & a_{6,4} & \cdots & * & * \\ \end{array}\right] \tag{2} \end{align*} \]
なお式(2)中の'*'(アスタリスク)は元の行列には含まれない要素であり、FORTRANコードへの渡すときは任意の値をとる。
正方行列の場合と違い、バンドマトリックスのときにはサブルーチンにより行列の格納方法がそれぞれ異なっており、ルーチン名をそのまま入れ替えることはできない。この点で呼び出し側を含めて設計の当初から考慮しなければならず、また使用するバンドマトリックスの解法をひとつに、あらかじめ決めておかないといけない。 この点で不便さは残る。
バンドマトリックスの解法
係数行列としてバンドマトリックスとなる連立一次方程式の解法で、図書・文献などでソースコードが利用可能な解法を調べた。
解法の簡単な概要を表1に示す。なおコード名は原則としてサブルーチン名を採用した。なお後退代入部分も別名ルーチンとなっているものもあるが表示していない。
| コード名 | 出典 | 概要 |
|---|---|---|
| mkl-LIB | 7) | Intel MKL Library,DGBTRF+DGBTRS,実行時メモリ異常 |
| DLIGB2 | 3) | LU分解 |
| DLICB2 | 3) | 改訂コレスキー法、N大きいとき精度悪い |
| BAND | 8) | ガウスジョルダン法 |
| BGLU1 | 10) | ガウス法 |
| BGLU2 | 10) | ガウス法(二段同時) |
| BGLU4 | 10) | ガウス法(二段二列同時) |
| BSLU1 | 10) | 対称帯ガウス法、N大きいとき精度悪い |
| BSLU2 | 10) | 対称帯ガウス法(二段同時)、N大きいとき精度悪い |
| BSLU4 | 10) | 対称帯ガウス法(二段二列同時)、N大きいとき精度悪い |
| BHLU1 | 10) | Martin-Wilkinson特殊ガウス |
| BHLU2 | 10) | Martin-Wilkinson特殊ガウス(二段同時) |
| BHLU4 | 10) | Martin-Wilkinson特殊ガウス(二段二列同時) |
| BANDEC | 9) | LU分解 |
先頭の'mkl-LIB'は、Intel Visual Fortran(IVF)のMath Kernel Library(MKL)にあるコード(MKLはBLAS、LAPACKなど数学ライブラリをIntelがパッケージ化したもの)を使用した。
これら各種ルーチンの、バンド行列の与え方は千差万別であり、典型的には(2)式のように与える。また作業用配列を係数行列と同じ変数名に割り当て、そのサイズを大きくすることで作業領域を確保するルーチンもある。
表1に示すルーチンは、N=4,NLD=NUD=1のような小規模なバンドマトリックスの例題を用いデバッグを実施した。小規模なスケールの計算ではすべて結果に異常は見られなかった。 表1の概要欄に Nが1000のオーダーになるとき、計算が不安定になったり解の精度が劣る結果が得られるなど正常とは思われないルーチンが一部存在する。原因究明はしていない。
解法の計算速度比較
上述の各種ルーチンについて、未知数の数N を種々変えて、バンドマトリックスとなる連立一次方程式の解を求め、その実行時間(CPU時間)を計測し、比較した。 比較の例題として、正方行列の場合の連立一次方程式の解法のときに使用した例題とほぼ同一の例題1を採用した。バンドマトリックスの要素設定のため、NLD とNUD は等しいとし入力データとして与え、要素を設定した。 得られたバンドマトリックスは式からわかるように対称行列となっている。
実行時間の比較を、表2に示す。Nが大きいとき不安定になったり解の精度が悪い解法は計測しておらず、実行時間をゼロとしている。
また計測は、Windows 7 (64bit OS)のDos Prompt(32bitアプリ用)上で実行し、コンパイラーはIVF Ver 13.1.1.171を用い、コンパイルオプションは次のように自動並列化のみを実施し、OpenMPによる最適化は実施していない。
リンク時のMKLルーチンのライブラリは同じく上のリストに示す並列化版を採用した。
| N(未知数の数) | 1000 | 2000 | 4000 | 8000 | 16000 | ||
|---|---|---|---|---|---|---|---|
| NLD=NUD(バンド幅) | 5 | 10 | 20 | 40 | 80 | Remarks | |
| 1 | mkl-LIB | 0 | 0 | 0 | 0 | 0 | メモリ異常 |
| 2 | DLIGB2 | 0 | 0 | 10 | 60 | 420 | |
| 3 | DLICB2 | 0 | 0 | 0 | 0 | 0 | 精度不足 |
| 4 | BAND | 0 | 0 | 20 | 150 | 800 | |
| 5 | BGLU1 | 0 | 0 | 0 | 50 | 190 | |
| 6 | BGLU2 | 0 | 0 | 10 | 50 | 270 | |
| 7 | BGLU4 | 0 | 0 | 10 | 40 | 220 | |
| 8 | BSLU1 | 0 | 0 | 0 | 0 | 0 | 精度不足 |
| 9 | BSLU2 | 0 | 0 | 0 | 0 | 0 | 精度不足 |
| 10 | BSLU4 | 0 | 0 | 0 | 0 | 0 | 精度不足 |
| 11 | BHLU1 | 0 | 0 | 10 | 60 | 310 | |
| 12 | BHLU2 | 0 | 10 | 10 | 40 | 180 | |
| 13 | BHLU4 | 0 | 0 | 10 | 40 | 180 | |
| 14 | BANDEC | 0 | 10 | 20 | 130 | 640 |
正方行列のときの実行時間の比較では、Intel MKLが圧倒的に速い。しかし、バンドマトリックスの場合には計算不能となり、比較の対象にはならない。 計算不能の原因を多少表面的に調査したが、内部のアルゴリズムなどLAPACKのソース自体を詳細に調べる必要があり、それ以上の追求は断念した。計算不能の現象を 次節に記す。
なお、ルーチンの実行時間はリスト1に示すように、バンドマトリックスの要素を設定する部分、右辺を計算する部分は計測時間に入れておらず、純粋にバンドマトリックスとなる連立一次方程式を解く部分の計算時間を測定している。 ただし、Window 7上で実行しており、バックグラウンドでプロセスが稼働している可能性があり、環境により値はバラツク可能性がある。なおこれら一連の計測は連続して自動実行しており、同一のバッチで計算したものである(日を違えて実行している訳ではない)。
LAPACKのバンドマトリックス解法
IntelのMKLをリンクさせて、N=2000の場合にDos Prompt上で実行すると、実行途中に図1に示す実行時のメッセージボックスが表示される。 このメッセージボックスはWindows 7のシステムからのエラーメッセージであり、表示後デバッグするかしないかのメッセージが表示される。 引数の間違いや警告、ゼロ割などシステム割り込みははDos Prompt上に出力されるが、図のメッセージはWindows OSのAPIを利用したときのエラーメッセージ、メモリのアロケーションや実行時の配列の範囲外書き込みによる破壊などのエラーではと推察される。
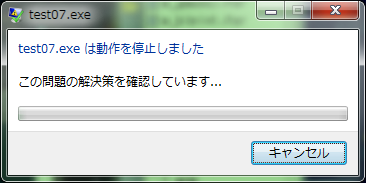
図1:Win7のエラーメッセージ
また、MKLのオリジナルであるLAPACKのソースコード DGBTRF, DGBTRS およびこれらルーチンから呼び出されるサブルーチン、関数(一部BLASのパッケージ)をソースとしてコンパイルリンクして、同じ現象が起こるかを確認した。必要なルーチン一式をリスト2に示す。
LAPACK およびBLAS のソースコードを用いコンパイル・リンクすると、ほとんどの場合図1に示すエラーメッセージが表示されるが、たまに条件によりメッセージ表示されず正解が求まることがある。 たまにエラーメッセージが表示されない場合とは、コンパイルオプションで "/Od"(最適化なし)で実行後、"/O3 /parallel /Zi"で速度最適化で再リンク後の初回実行時にはまともに計算を実行する。2度目の実行では図1のエラーメッセージが表示される。 これも再現性がなく、どんな条件のときにエラーとなるかいまだ判明していない。
バンドマトリックスの解法まとめ
詳細な原因究明を実施していないが、Intel MKLライブラリの解法の圧倒的速さを期待したのであるが、意外にも計算が安定しないという結果になった。 使用方法に問題があるのかも知れないが、今後、調査・原因究明をしたい。またMKLライブラリ以外に、大規模行列には小国らの一連の高速解法(BGLUn,BHLUn)が速度的に有利であることが分かった。
正方行列の解法についてはIntelは力を注いでいるのかもしれないが、バンドマトリックスの解法はほったらかしにされている可能性がある。 現実の工学での利用場面は圧倒的に少ないこともあるが、反応器シミュレーションを行うには高速解法が是非とも必要である。
サンプルコード、関連ファイルのダウンロードは、こちら(未リンク)で取り扱っています。
Literature Cited
連立一次方程式の解法のソースコード、ライブラリが掲載されている図書・出典を以下に示す。
- 引用文献・参考図書
- 1) 島崎著:「スーパーコンピュータとプログラミング」、共立出版(1989).
- 2) 村田、小国、唐木著:「スーパーコンピュータ」、丸善(1986).
- 3) 渡部、名取、小国著:「数値解析とFORTRAN」第3版、丸善(1983).
- 4) 牛島著:「OpenMPによる並列プログラミングと数値計算法」、丸善(2006).
- 5) 戸川隼人著:「新装版 科学技術計算ハンドブック基礎篇C言語版」、サイエンス社(2002).
- 6) インテル:マス・カーネル・ライブラリー(Intel MKL).
- 7) LAPACK:Linear Algebra PACKage, Netlib(www.netlib.org).
- 8) 大野、磯田監修: 「新版 数値計算ハンドブック」P.16、オーム社(1990)
- 9) Press,W.H.,S.A.Teukolsky,W.T.Vetterling,B.P.Flannery:"Numerical Recipes in FORTRAN 77",2nd Ed.,Cambridge Univ.Press.(2001).
- 10) 小国力編著:「行列計算ソフトウェア、WS,スーパーコン、並列計算機」、丸善(1991).
