数値解析：スティッフな連立微分方程式

トップ > ライブラリ > 数値解析 > スティッフな連立微分方程式

数値解析：スティッフな連立微分方程式

現在工事中です。微分方程式が特殊なタイプである”スティッフな微分方程式”となるときの解法を以下紹介します。

1. スティッフな微分方程式とは

1.1 Stiffな微分方程式のサンプル

2. スティッフな微分方程式の解法

2.1 IMSLによる解法（ルーチン）
2.2 VODEによる解法
2.3 ODEPACKによる解
2.4 IMSLのGear法による解
2.5 Semi-Implicit Runge-Kutta (3step)法による解

3. そのほかの例題

3.1 例題２：連立微分方程式の解法
3.2 例題３¹¹⁾：連立微分方程式の解法
3.3 例題４¹¹⁾：連立微分方程式の解法
3.4 例題５⁷⁾：連立微分方程式の解法

4. 化学工学への応用
5. 例題ほかの解答
6. Literature Cited

【注】数式表示にはMathJaxを利用しています。IE8以下では表示が遅くなる可能性があります。FireFox などIE8以外のブラウザを利用下さい。

先頭に戻る

スティッフな微分方程式とは

連立微分方程式の中には、"Stiffな微分方程式"（日本語で「硬い微分方程式」）と呼ばれる特殊な微分方程式が存在する。通常の陽解法はもちろん、ステップ幅可変の陽解法でも解くことが難しい微分方程式問題である。化学工学では、例えば、気相のメタン燃焼（メタンの酸化反応）のようにラジカル種の素反応を考慮する場合、その素反応の数が数十から百数十個存在し、その反応速度が極めて速い素反応から遅い素反応まで混在する反応問題を解くとき、Stiffな微分方程式に相当する。

また、２つの並列反応があり、片方の反応が早く、もう片方が遅いとき、速い反応に合わせて固定時間刻みを小さくすると、遅い反応を解くのに極めて膨大なステップ数を経ないと解に到達しないことがある。可変刻みで解くこともあるがこのような特異な微分方程式を解くのは無限の計算時間を必要とし、やはりStiffな微分方程式となる。

こうしたStiffな微分方程式を解くための特殊な解法が、種々用意されている。基本的には可変ステップ幅を用い、陰解法もしくは半陰解法を用いた解法が多い。これら解法の比較やスティッフな微分方程式の解法の詳細については、以下取り扱う。

数学的な "Stiffな方程式" の定義¹¹⁾は、yを m次元の従属変数ベクトルとしたとき、(1)式で表される連立一次常微分方程式の係数行列 Aの固有値 λi(i=1,m)を考えるとき、 \[ \begin{align*} & {\bf y'} = {\bf Ay }+ {\bf \phi} (x) \tag{1} \\ & {\rm BC} \quad {\bf y}(x_0) = {\bf y_0} \\ \end{align*} \]

行列の固有値が、 \[ \begin{align*} & (a) \quad {\rm Re}( \lambda _i) < 0 \quad for \> all \> \lambda_i \tag{2} \\ & (b) \quad {\rm max} \; | {\rm Re}( \lambda _i) | >> {\rm min} \; |{\rm Re}( \lambda _i)| \tag{3} \\ \end{align*} \] の２つの条件を満足するとき、"Stiff"という。

Stiffな微分方程式のサンプル

Stiffな微分方程式のサンプルとして、後述する例題１を取り上げる。 \[ \left . \eqalign { \begin{align*} y_1' & = -0.1y_1-49.9y_2 \\ y_2' & = -50y_2 \\ y_3' & = 70y_2-120y_3 \\ \end{align*} } \right\} \tag{4} \\ \]

係数行列Aは、３行３列の正方行列となる。 \[ \begin{align*} {\bf A} = \left[ \begin{array}{ccc} -0.1 & -49.9 & 0 \\ 0 & -50 & 0 \\ 0 & -70 & -120 \\ \end{array} \right] \tag{5} \end{align*} \]

行列Aの固有値λは、行列式 (A-Iλ)=0を解き、 \[ \begin{align*} \left. \eqalign{ {\rm det} \big| {\bf A}-{\bf I} \; \lambda \big| & = (-0.1-\lambda)(-50-\lambda)(-120-\lambda) = 0 \\ \lambda & = -0.1,-50,-120 } \right. \tag{6} \end{align*} \]

が得られる。すべての固有値が負であり、固有値の実数部分の絶対値の最大のものが120、最小のものが0.1と上の条件(2)、(3)式をともに満足しているといえる。従って連立微分方程式(4)はStiffな微分方程式とみなすことができる。

先頭に戻る

スティッフな微分方程式の解法

Stiffな微分方程式の解法（ソースコード）として、次のものがある。1-4は、privateに開発または入手したもの、 5-7は、Compaq Fortranに付属のIMSLライブラリ、9-10はODEPACKとしてインターネット公開、11-12は図書⁷⁾による公開、 13-14はVODE packとしてインターネット公開されたものである。 Adams法ほか一部は、Stiffな微分方程式用ではないがStiffな程度により解ける可能性がある。

Stiffな微分方程式の解法一覧
1) Gear（Private）
2) Adams（Private）
3) Semi-implicit Runge-Kutta法（2-step,Private）
4) Semi-implicit Runge-Kutta法（3-step,Private）
5) Adams-Molton法（IMSL Library）
6) Gear法（IMSL Library）
7) Petzold-Gear法（IMSL Library）
8) Adams（odepack）
9) Gear（odepack）
10) LSODE（odepack、Auto BDF）
11) Rosenbrook（Recipe 77）
12) Bulirsch-Stoer（Recipe 77）
13) Adams（VODE pack）
14) BDF（VODE pack）

残念ながら、IntelのMKL(Math Kernel Library)には、Stiffな微分方程式の解法ライブラリはなく、もっとも単純なRunge-Kutta法ですら用意されていない。どちらかというと線形計算（連立方程式の高速解法）の BLASやLAPACK関連を収録している。Intel Fortranを主コンパイラーとして用いるなら、IMSLライブやほかの市販ライブラリを用意する必要がある。またはソースコードを入手しておく必要がある。

Gear法は、図書¹²⁾にコードが記述されているが、そのままではうまく動かない（らしい？）。

ODEPACKとVODEは、ともにLLNL(Lawrence Livermore National Laboratory)の A. C. Hindmarshらが開発したもので、共通のルーチンを利用している。また引数もほぼ共通している。 ODEPACKの方が新しい。14)のBDFとは、Backward Differentiation Formulasの意味で陰解法ベース。また13)のADAMS法も陰解法ベースではあるが、Stiff専用の解法ではない。

これら解法を、実際の例題に適用したときの解を以下比較する。

先頭に戻る

IMSLによる解法（ルーチン）

V.Numerics社のIMSLライブラリにある、Gear法関連のルーチン IVPAGをマニュアルから抜粋して紹介する。このルーチンはフラグによりAdams-Moulton法またはGearのBDF法(Backward Differentiation Formula)を選択できる。引数の並びは次のとおり。


CALL IVPAG (IDO, N, FCN, FCNJ, A, T, TEND, TOL, PARAM, Y)

Gear法の使い方は、後出するVODE、ODEPACKのGear法とほぼ同等で、初回の設定、出力点まで自動刻みで計算を行う。解法は最大５次まで精度を保ち、自動刻み幅をによる陰解法を採用している。なお引数の詳細な説明はIMSLのマニュアルを参照されたい。

ルーチンIVPAGの引数
引数	引数の説明
IDO:	計算を制御するフラグ、およびステイタス出力
N:	連立微分方程式の元数
FCN:	連立微分方程式の右辺ベクトルを計算する関数ルーチン
FCNJ:	右辺ベクトルのヤコビアン計算ルーチン
A:	連立微分方程式左辺の行列（陰的な微分方程式のとき）
T:	独立変数値（入力は初期値、出力はTEND値）
TEND:	解を求める独立変数値
TOL:	計算精度を制御する判定条件
PARAM:	オプションパラメータを入力する配列
Y:	従属変数配列、入力は初期値、出力はTEND点の計算値

なお、IMSLライブラリはCompaq Visual Fortran（以下CVF）Ver 6.6Bに同梱しているライブラリを参考にしている。最新版ではないことに注意されたい。 CVFは現在販売されていない。Intel Visual Fortranに置換されつつある。Intel Visual Fortran用の最新のIMSLライブはオプションで購入できる。 Intel Visual Fortran付属のMKL（Math Kernel Library）は主に線形計算を取り扱うライブラリで、微分方程式の一般的な解法を含め用意されていない。特殊関数（例えばベッセル関数、誤差関数など）もサポートしていない。

先頭に戻る

VODEによる解法

これら各種のツールの使い方を説明するため、VODEを例にとり、例題１をAdams法、BDF法で、次の例題１を解くことを考える。

例題１：スティッフな微分方程式の解

次の連立微分方程式をスティッフな解法を用いて、ステップ幅0.1とし、ステップ数100まで解きなさい。なお初期刻み幅を1.E-5とする。 \[ \left . \eqalign { \begin{align*} y_1' & = -0.1y_1-49.9y_2 \\ y_2' & = -50y_2 \\ y_3' & = 70y_2-120y_3 \\ \end{align*} } \right . \tag{A.1} \\ \] 初期条件は、次のとおり。 \[ \left . \eqalign { \begin{align*} y_1(0) & = 2 \\ y_2(0) & = 1 \\ y_3(0) & = 2 \\ \end{align*} } \right . \tag{A.2} \\ \] なお、解析解は次のとおり。 \[ \left . \eqalign { \begin{align*} y_1(t) & = \exp(-0.1t)+\exp(-50t) \\ y_2(t) & = \exp(-50t) \\ y_3(t) & = \exp(-50t)+\exp(-120t) \\ \end{align*} } \right . \tag{A.3} \]

例題１は、上の(4)式の係数行列を持ち、その固有値の絶対値の最小と最大が0.1と120であり、Stiffな微分方程式とみなされる。これをVODE法のサブルーチンを使い解くことを考える。 VODE法のソースコードに引数の受け渡し方が記述されており、その通りに入力すればいいのであるが、ここでは例題１を解くときのルーチンを示す。

メインルーチンから、リスト１に示すVODE Packを使うためのルーチンDVODEを呼び出す。そのとき次の引数をセットし、呼び出す。

引数の説明
ISWTCH: 問題のフラグ、例題１のときISWTCH=1が入る
ISW2: =1のときAdams法、 =2のときBDF法

リスト１：dvode.for


c-----------------------------------------------------------------------
      subroutine   DVODE( ISWTCH,ISW2 )
c
c
c
      INCLUDE      'COMMON.H'
      parameter    (LRW=70,LIW=35)
      DIMENSION    Y(3),YANA(3),RWORK(LRW),IWORK(LIW),
c  RPAR(i),IPAR(i): User defined work array
     1             RPAR(10),IPAR(10),EPSA(3)
      INTEGER*2    IH,IM,IS,ISS
      EXTERNAL     FUN2,JAC4
!
!  X : 独立変数
!  Y(i),i=1,N : 従属変数
!  N : 従属変数の数
!  EPS1 : 絶対誤差の判定値
!  EPS2 : 相対誤差の判定値
!
      call         INIT( X,Y,N,EPS1,EPS2 )	! 初期値などを設定

      ITOL=1
      EPSR=EPS2		! relative tolerance
      DO I=1,N
        EPSA(I)=EPS1	! absolue tolerance
      END DO
c
      ITASK=1		! normal computation
      ISTATE=1		! First call
C
      IOPT=1		! No optional inputs
      if(ISW2.eq.1) then
        MF=10		! nonstiff(Adams) method
        write(nwrt,*) ' ----- nonstiff(Adams) by VODE.for -----'
      elseif(ISW2.eq.2) then
        MF=21		! stiff(BDF), user-supplied full jacobian
        write(nwrt,*)
     1   ' ----- stiff(Backward Diff.Form) by VODE.for -----'
      endif
!  初期値 X=X0 の解析解を計算
      CALL         ANAL( X,YANA )
      write(nwrt,'(a15,3i5,2e15.8,6e15.8)') ' IS,NS,NQ,X,H = ',
     1 ISTATE,NST,NQU,X,HNOW,(Y(J),J=1,N),(YANA(J),J=1,N)
C
      CALL         COND( H,XSTEP,NSTEP )	! 刻み幅、ステップ数を設定
      RWORK(5)=H	! 初期刻み幅、
      IWORK(6)=1000	! MAX STEP
      CALL         GETTIM( IH,IM,IS,ISS )
      CPU=DBLE(ISS)/100.D0+DBLE(IS+(IM+IH*60)*60)	! SEC
C
      DO 40 I=1,NSTEP		! ステップ数NSTEPまで繰り返す
      XEND=XSTEP*DBLE(I)	! 現在のステップの最終時刻
c
c  VODE、刻み幅可変の陰解法、刻み幅を変えながら時刻XENDまで積分
c
      call m_dvode( FUN2,N,Y,X,XEND,ITOL,EPSR,EPSA,ITASK,
     1            ISTATE,IOPT,RWORK,LRW,IWORK,LIW,JAC4,MF,
     2            RPAR,IPAR)
      HNOW=RWORK(11)	! step size last used
      NST=IWORK(11)	! step number last used
      NQU=IWORK(14)	! method order last used
      IF(ISTATE.NE.2) then
        write(nwrt,*) ' ISTATE = ',ISTATE
        stop
      endif
C
      CALL         ANAL( X,YANA )	! 現時刻の解析解を計算
      write(nwrt,'(a15,3i5,2e15.8,6e15.8)') ' IS,NS,NQ,X,H = ',
     1 ISTATE,NST,NQU,X,HNOW,(Y(J),J=1,N),(YANA(J),J=1,N)
C
   40 CONTINUE
      CALL         GETTIM( IH,IM,IS,ISS )
      CCPU=DBLE(ISS)/100.D0+DBLE(IS+(IM+IH*60)*60)	! SEC
      CCPU=CCPU-CPU
      WRITE(NWRT,1005) CCPU
      RETURN
 1005 FORMAT(2X,' CPU(SEC) = ',1PF15.2)
      END

DVODEルーチンから呼び出されるルーチンを次表に示す。またルーチンの中身をリスト２およびリスト３に示す。

DVODE中の呼び出しルーチン
ルーチン名	ルーチンの説明
FUN2	連立微分方程式の右辺を計算する
JAC4	連立微分方程式の係数行列の微分（ヤコビ行列）を返す
INIT	初期値を設定する
ANAL	解析解を計算する
COND	解法で使う条件を設定する

リスト２：FUN2とJAC4ルーチン


C---------------------------------------------------------------
      SUBROUTINE   FUN2( N,X,Y,YP,RPAR,IPAR )
C
c  RPAR(i),IPAR(i): User defined work array
c
      INCLUDE      'COMMON.H'
      DIMENSION    Y(1),YP(1),RPAR(10),IPAR(10)
      CALL         FUN( X,Y,YP )
      RETURN
      END
c-----------------------------------------------------------------------
      SUBROUTINE   FUN( X,Y,YP )
C
C  CALC.  DY/DX=FUN(X,Y)
C
      INCLUDE      'COMMON.H'
      DIMENSION    Y(1),YP(1)

      IF(ISW.EQ.1) THEN
        YP(1)=-0.1D0*Y(1)-49.9D0*Y(2)	! 連立微分方程式の右辺を計算
        YP(2)=-50.0D0*Y(2)
        YP(3)=70.0D0*Y(2)-120.0D0*Y(3)
      ELSEIF(ISW.EQ.2) THEN
         ･･･
        途中省略
         ･･･
      ENDIF
      RETURN
      END
C----------------------------------------------------------------
      SUBROUTINE   JAC4( K,X,Y,ML,MU,PD,NROWPD,RPAR,IPAR )
C
      INCLUDE      'COMMON.H'
      DIMENSION    Y(1),PD(NROWPD,*),RPAR(10),IPAR(10)
      CALL         JAC( X,Y,PD,K )	! ヤコビアン行列を計算
      RETURN
      END
C----------------------------------------------------------------
      SUBROUTINE   JAC( X,Y,PD,K )
C
C  CALC. JACOBIAN
C
      INCLUDE      'COMMON.H'
      DIMENSION    Y(1),PD(K,K)

      IF(ISW.EQ.1) THEN
        PD(1,1)=-0.1D0
        PD(1,2)=-49.9D0
        PD(1,3)=0.0D0
        PD(2,1)=0.0D0
        PD(2,2)=-50.0D0
        PD(2,3)=0.0D0
        PD(3,1)=0.0D0
        PD(3,2)=70.0D0
        PD(3,3)=-120.0D0
      ELSEIF(ISW.EQ.2) THEN
         ･･･
        途中省略
         ･･･
      ENDIF
      RETURN
      END

FUNおよびJACルーチンは、それぞれ連立微分方程式の右辺を計算、係数のヤコビ行列を計算するおおもとのルーチンである。 FUN2、JAC4ルーチンは、それぞれ解法特有の引数並びがあり、それを調整するための中間ルーチンである。

リスト３：その他ルーチン


C----------------------------------------------------------------
      SUBROUTINE   INIT( X,Y,NVAR,EPSA,EPSR )
C
C  SET INITIAL VALUE
C
      INCLUDE      'COMMON.H'
      DIMENSION    Y(1)
C
      X=ZERO
      IF(ISW.EQ.1) THEN
        Y(1)=2.D0 ; Y(2)=1.D0 ; Y(3)=2.D0 ; NVAR=3	! 初期値
        EPSA=0.D0 ; EPSR=1.D-6	! 絶対誤差、相対誤差の判定値
      ELSEIF(ISW.EQ.2) THEN
         ･･･
        途中省略
         ･･･
      ENDIF
      RETURN
      END
c-----------------------------------------------------------------------
      SUBROUTINE   COND( HINI,XSTEP,NSTEP )
C
C  SET STEP
C
      INCLUDE      'COMMON.H'
      IF(ISW.EQ.1) THEN
!   HINI : 可変刻みの刻み初期値
!  XSTEP : 出力用のステップ幅
!  NSTEP : 出力のステップ数
        HINI=1.D-5 ; XSTEP=0.1D0 ; NSTEP=100
      ELSEIF(ISW.EQ.2) THEN
         ･･･
        途中省略
         ･･･
      ENDIF
      RETURN
      END
C----------------------------------------------------------------
      SUBROUTINE   ANAL( X,Y )
C
C  SET ANALYTICAL SOLUTION
C
      INCLUDE      'COMMON.H'
      DIMENSION    Y(1)
C
      IF(ISW.EQ.1) THEN
        Y(1)=EXP(-0.1D0*X)+EXP(-50.D0*X)
        Y(2)=EXP(-50.D0*X)
        Y(3)=EXP(-50.D0*X)+EXP(-120.D0*X)
      ELSEIF(ISW.EQ.2) THEN
         ･･･
         ･･･
      ENDIF
      RETURN
      END

INITルーチンで、解法の初期値、変数の数、収束判定条件を設定し、CONDルーチンで初期刻み幅、出力ステップ幅、ステップ数を設定している。 ANALルーチンは解析解を計算するルーチンである。

例題１をVODEのBDF法（MF=21）のときの出力をリスト４に示す。解析解と数値解の差はわずか0.06%以下である。

リスト４：VODEのBDF法による出力


 isw,ind =     1   14
  ----- stiff(Backward Diff.Form) by VODE.for -----
                  IS   NS   NQ           X              H              Y(1)           Y(2)           Y(3)        YANA(1)        YANA(2)        YANA(3)
 IS,NS,NQ,X,H =    1    0    0 0.00000000E+00 0.00000000E+00 0.20000000E+01 0.10000000E+01 0.20000000E+01 0.20000000E+01 0.10000000E+01 0.20000000E+01
 IS,NS,NQ,X,H =    2   89    5 0.10000000E+00 0.18092544E-02 0.99678781E+00 0.67379776E-02 0.67441284E-02 0.99678778E+00 0.67379470E-02 0.67440912E-02
 IS,NS,NQ,X,H =    2  145    5 0.20000000E+00 0.18092544E-02 0.98024407E+00 0.45400415E-04 0.45400452E-04 0.98024407E+00 0.45399930E-04 0.45399968E-04
 IS,NS,NQ,X,H =    2  200    5 0.30000000E+00 0.18092544E-02 0.97044584E+00 0.30590747E-06 0.30590747E-06 0.97044584E+00 0.30590232E-06 0.30590232E-06
 IS,NS,NQ,X,H =    2  255    5 0.40000000E+00 0.18092544E-02 0.96078944E+00 0.20612010E-08 0.20612010E-08 0.96078944E+00 0.20611536E-08 0.20611536E-08
 IS,NS,NQ,X,H =    2  310    5 0.50000000E+00 0.18092544E-02 0.95122942E+00 0.13888348E-10 0.13888348E-10 0.95122942E+00 0.13887944E-10 0.13887944E-10
 IS,NS,NQ,X,H =    2  366    5 0.60000000E+00 0.18092544E-02 0.94176453E+00 0.93579527E-13 0.93579527E-13 0.94176453E+00 0.93576230E-13 0.93576230E-13
 IS,NS,NQ,X,H =    2  421    5 0.70000000E+00 0.18092544E-02 0.93239382E+00 0.63053777E-15 0.63053777E-15 0.93239382E+00 0.63051168E-15 0.63051168E-15
 IS,NS,NQ,X,H =    2  476    5 0.80000000E+00 0.18092544E-02 0.92311635E+00 0.42485562E-17 0.42485562E-17 0.92311635E+00 0.42483543E-17 0.42483543E-17
 IS,NS,NQ,X,H =    2  532    5 0.90000000E+00 0.18092544E-02 0.91393119E+00 0.28626721E-19 0.28626721E-19 0.91393119E+00 0.28625186E-19 0.28625186E-19
 IS,NS,NQ,X,H =    2  587    5 0.10000000E+01 0.18092544E-02 0.90483742E+00 0.19288652E-21 0.19288652E-21 0.90483742E+00 0.19287498E-21 0.19287498E-21
 IS,NS,NQ,X,H =    2  642    5 0.11000000E+01 0.18092544E-02 0.89583414E+00 0.12996671E-23 0.12996671E-23 0.89583414E+00 0.12995814E-23 0.12995814E-23
 IS,NS,NQ,X,H =    2  697    5 0.12000000E+01 0.18092544E-02 0.88692044E+00 0.87571419E-26 0.87571419E-26 0.88692044E+00 0.87565108E-26 0.87565108E-26
 IS,NS,NQ,X,H =    2  753    5 0.13000000E+01 0.18092544E-02 0.87809543E+00 0.59005520E-28 0.59005520E-28 0.87809543E+00 0.59000905E-28 0.59000905E-28
 IS,NS,NQ,X,H =    2  808    5 0.14000000E+01 0.18092544E-02 0.86935824E+00 0.39757851E-30 0.39757851E-30 0.86935824E+00 0.39754497E-30 0.39754497E-30
 IS,NS,NQ,X,H =    2  863    5 0.15000000E+01 0.18092544E-02 0.86070798E+00 0.26788794E-32 0.26788794E-32 0.86070798E+00 0.26786370E-32 0.26786370E-32
 IS,NS,NQ,X,H =    2  918    5 0.16000000E+01 0.18092544E-02 0.85214379E+00 0.18050258E-34 0.18050258E-34 0.85214379E+00 0.18048514E-34 0.18048514E-34
 IS,NS,NQ,X,H =    2  974    5 0.17000000E+01 0.18092544E-02 0.84366482E+00 0.12162243E-36 0.12162243E-36 0.84366482E+00 0.12160993E-36 0.12160993E-36
 IS,NS,NQ,X,H =    2 1029    5 0.18000000E+01 0.18092544E-02 0.83527021E+00 0.81949051E-39 0.81949051E-39 0.83527021E+00 0.81940126E-39 0.81940126E-39
 IS,NS,NQ,X,H =    2 1084    5 0.19000000E+01 0.18092544E-02 0.82695913E+00 0.55217175E-41 0.55217175E-41 0.82695913E+00 0.55210823E-41 0.55210823E-41
 IS,NS,NQ,X,H =    2 1139    5 0.20000000E+01 0.18092544E-02 0.81873075E+00 0.37205268E-43 0.37205268E-43 0.81873075E+00 0.37200760E-43 0.37200760E-43
 IS,NS,NQ,X,H =    2 1195    5 0.21000000E+01 0.18092544E-02 0.81058425E+00 0.25068866E-45 0.25068866E-45 0.81058425E+00 0.25065675E-45 0.25065675E-45
 IS,NS,NQ,X,H =    2 1250    5 0.22000000E+01 0.18092544E-02 0.80251880E+00 0.16891373E-47 0.16891373E-47 0.80251880E+00 0.16889119E-47 0.16889119E-47
 IS,NS,NQ,X,H =    2 1305    5 0.23000000E+01 0.18092544E-02 0.79453360E+00 0.11381387E-49 0.11381387E-49 0.79453360E+00 0.11379799E-49 0.11379799E-49
 IS,NS,NQ,X,H =    2 1361    5 0.24000000E+01 0.18092544E-02 0.78662786E+00 0.76687655E-52 0.76687655E-52 0.78662786E+00 0.76676481E-52 0.76676481E-52
 IS,NS,NQ,X,H =    2 1416    5 0.25000000E+01 0.18092544E-02 0.77880078E+00 0.51672053E-54 0.51672053E-54 0.77880078E+00 0.51664206E-54 0.51664206E-54
 IS,NS,NQ,X,H =    2 1471    5 0.26000000E+01 0.18092544E-02 0.77105159E+00 0.34816570E-56 0.34816570E-56 0.77105159E+00 0.34811068E-56 0.34811068E-56
 IS,NS,NQ,X,H =    2 1526    5 0.27000000E+01 0.18092544E-02 0.76337949E+00 0.23459364E-58 0.23459364E-58 0.76337949E+00 0.23455513E-58 0.23455513E-58
 IS,NS,NQ,X,H =    2 1582    5 0.28000000E+01 0.18092544E-02 0.75578374E+00 0.15806892E-60 0.15806892E-60 0.75578374E+00 0.15804201E-60 0.15804201E-60
 IS,NS,NQ,X,H =    2 1637    5 0.29000000E+01 0.18092544E-02 0.74826357E+00 0.10650666E-62 0.10650666E-62 0.74826357E+00 0.10648787E-62 0.10648787E-62
 IS,NS,NQ,X,H =    2 1692    5 0.30000000E+01 0.18092544E-02 0.74081822E+00 0.71764061E-65 0.71764061E-65 0.74081822E+00 0.71750960E-65 0.71750960E-65
 IS,NS,NQ,X,H =    2 1747    5 0.31000000E+01 0.18092544E-02 0.73344696E+00 0.48354540E-67 0.48354540E-67 0.73344696E+00 0.48345416E-67 0.48345416E-67
 IS,NS,NQ,X,H =    2 1803    5 0.32000000E+01 0.18092544E-02 0.72614904E+00 0.32581233E-69 0.32581233E-69 0.72614904E+00 0.32574885E-69 0.32574885E-69
 IS,NS,NQ,X,H =    2 1858    5 0.33000000E+01 0.18092544E-02 0.71892373E+00 0.21953197E-71 0.21953197E-71 0.71892373E+00 0.21948785E-71 0.21948785E-71
 IS,NS,NQ,X,H =    2 1913    5 0.34000000E+01 0.18092544E-02 0.71177032E+00 0.14792039E-73 0.14792039E-73 0.71177032E+00 0.14788975E-73 0.14788975E-73
 IS,NS,NQ,X,H =    2 1969    5 0.35000000E+01 0.18092544E-02 0.70468809E+00 0.99668583E-76 0.99668583E-76 0.70468809E+00 0.99647330E-76 0.99647330E-76
 IS,NS,NQ,X,H =    2 2024    5 0.36000000E+01 0.18092544E-02 0.69767633E+00 0.67156575E-78 0.67156575E-78 0.69767633E+00 0.67141843E-78 0.67141843E-78
 IS,NS,NQ,X,H =    2 2079    5 0.37000000E+01 0.18092544E-02 0.69073433E+00 0.45250023E-80 0.45250023E-80 0.69073433E+00 0.45239818E-80 0.45239818E-80
 IS,NS,NQ,X,H =    2 2134    5 0.38000000E+01 0.18092544E-02 0.68386141E+00 0.30489412E-82 0.30489412E-82 0.68386141E+00 0.30482350E-82 0.30482350E-82
 IS,NS,NQ,X,H =    2 2190    5 0.39000000E+01 0.18092544E-02 0.67705687E+00 0.20543730E-84 0.20543730E-84 0.67705687E+00 0.20538846E-84 0.20538846E-84
 IS,NS,NQ,X,H =    2 2245    5 0.40000000E+01 0.18092544E-02 0.67032005E+00 0.13842342E-86 0.13842342E-86 0.67032005E+00 0.13838965E-86 0.13838965E-86
 IS,NS,NQ,X,H =    2 2300    5 0.41000000E+01 0.18092544E-02 0.66365025E+00 0.93269538E-89 0.93269538E-89 0.66365025E+00 0.93246214E-89 0.93246214E-89
 IS,NS,NQ,X,H =    2 2355    5 0.42000000E+01 0.18092544E-02 0.65704682E+00 0.62844906E-91 0.62844906E-91 0.65704682E+00 0.62828805E-91 0.62828805E-91
 IS,NS,NQ,X,H =    2 2411    5 0.43000000E+01 0.18092544E-02 0.65050909E+00 0.42344824E-93 0.42344824E-93 0.65050909E+00 0.42333716E-93 0.42333716E-93
 IS,NS,NQ,X,H =    2 2466    5 0.44000000E+01 0.18092544E-02 0.64403642E+00 0.28531894E-95 0.28531894E-95 0.64403642E+00 0.28524233E-95 0.28524233E-95
 IS,NS,NQ,X,H =    2 2521    5 0.45000000E+01 0.18092544E-02 0.63762815E+00 0.19224757E-97 0.19224757E-97 0.63762815E+00 0.19219477E-97 0.19219477E-97
 IS,NS,NQ,X,H =    2 2577    5 0.46000000E+01 0.18092544E-02 0.63128365E+00 0.12953619E-99 0.12953619E-99 0.63128365E+00 0.12949982E-99 0.12949982E-99
 IS,NS,NQ,X,H =    2 2632    5 0.47000000E+01 0.18092544E-02 0.62500227E+00 0.87281332-102 0.87281332-102 0.62500227E+00 0.87256292-102 0.87256292-102
 IS,NS,NQ,X,H =    2 2687    5 0.48000000E+01 0.18092544E-02 0.61878339E+00 0.58810060-104 0.58810060-104 0.61878339E+00 0.58792827-104 0.58792827-104
 IS,NS,NQ,X,H =    2 2742    5 0.49000000E+01 0.18092544E-02 0.61262639E+00 0.39626150-106 0.39626150-106 0.61262639E+00 0.39614295-106 0.39614295-106
 IS,NS,NQ,X,H =    2 2798    5 0.50000000E+01 0.18092544E-02 0.60653066E+00 0.26700053-108 0.26700053-108 0.60653066E+00 0.26691902-108 0.26691902-108
 IS,NS,NQ,X,H =    2 2853    5 0.51000000E+01 0.18092544E-02 0.60049558E+00 0.17990465-110 0.17990465-110 0.60049558E+00 0.17984862-110 0.17984862-110
 IS,NS,NQ,X,H =    2 2908    5 0.52000000E+01 0.18092544E-02 0.59452055E+00 0.12121954-112 0.12121954-112 0.59452055E+00 0.12118105-112 0.12118105-112
 IS,NS,NQ,X,H =    2 2963    5 0.53000000E+01 0.18092544E-02 0.58860497E+00 0.81677587-115 0.81677587-115 0.58860497E+00 0.81651148-115 0.81651148-115
 IS,NS,NQ,X,H =    2 3019    5 0.54000000E+01 0.18092544E-02 0.58274825E+00 0.55034263-117 0.55034263-117 0.58274825E+00 0.55016111-117 0.55016111-117
 IS,NS,NQ,X,H =    2 3074    5 0.55000000E+01 0.18092544E-02 0.57694981E+00 0.37082023-119 0.37082023-119 0.57694981E+00 0.37069564-119 0.37069564-119
 IS,NS,NQ,X,H =    2 3129    5 0.56000000E+01 0.18092544E-02 0.57120906E+00 0.24985824-121 0.24985824-121 0.57120906E+00 0.24977276-121 0.24977276-121
 IS,NS,NQ,X,H =    2 3185    5 0.57000000E+01 0.18092544E-02 0.56552544E+00 0.16835419-123 0.16835419-123 0.56552544E+00 0.16829556-123 0.16829556-123
 IS,NS,NQ,X,H =    2 3240    5 0.58000000E+01 0.18092544E-02 0.55989837E+00 0.11343686-125 0.11343686-125 0.55989837E+00 0.11339666-125 0.11339666-125
 IS,NS,NQ,X,H =    2 3295    5 0.59000000E+01 0.18092544E-02 0.55432728E+00 0.76433623-128 0.76433623-128 0.55432728E+00 0.76406066-128 0.76406066-128
 IS,NS,NQ,X,H =    2 3350    5 0.60000000E+01 0.18092544E-02 0.54881164E+00 0.51500886-130 0.51500886-130 0.54881164E+00 0.51482002-130 0.51482002-130
 IS,NS,NQ,X,H =    2 3406    5 0.61000000E+01 0.18092544E-02 0.54335087E+00 0.34701237-132 0.34701237-132 0.54335087E+00 0.34688300-132 0.34688300-132
 IS,NS,NQ,X,H =    2 3461    5 0.62000000E+01 0.18092544E-02 0.53794444E+00 0.23381653-134 0.23381653-134 0.53794444E+00 0.23372793-134 0.23372793-134
 IS,NS,NQ,X,H =    2 3516    5 0.63000000E+01 0.18092544E-02 0.53259180E+00 0.15754531-136 0.15754531-136 0.53259180E+00 0.15748464-136 0.15748464-136
 IS,NS,NQ,X,H =    2 3571    5 0.64000000E+01 0.18092544E-02 0.52729242E+00 0.10615384-138 0.10615384-138 0.52729242E+00 0.10611232-138 0.10611232-138
 IS,NS,NQ,X,H =    2 3627    5 0.65000000E+01 0.18092544E-02 0.52204578E+00 0.71526336-141 0.71526336-141 0.52204578E+00 0.71497916-141 0.71497916-141
 IS,NS,NQ,X,H =    2 3682    5 0.66000000E+01 0.18092544E-02 0.51685133E+00 0.48194362-143 0.48194362-143 0.51685133E+00 0.48174917-143 0.48174917-143
 IS,NS,NQ,X,H =    2 3737    5 0.67000000E+01 0.18092544E-02 0.51170858E+00 0.32473305-145 0.32473305-145 0.51170858E+00 0.32460004-145 0.32460004-145
 IS,NS,NQ,X,H =    2 3793    5 0.68000000E+01 0.18092544E-02 0.50661699E+00 0.21880475-147 0.21880475-147 0.50661699E+00 0.21871378-147 0.21871378-147
 IS,NS,NQ,X,H =    2 3848    5 0.69000000E+01 0.18092544E-02 0.50157607E+00 0.14743039-149 0.14743039-149 0.50157607E+00 0.14736819-149 0.14736819-149
 IS,NS,NQ,X,H =    2 3903    5 0.70000000E+01 0.18092544E-02 0.49658530E+00 0.99338424-152 0.99338424-152 0.49658530E+00 0.99295904-152 0.99295904-152
 IS,NS,NQ,X,H =    2 3958    5 0.71000000E+01 0.18092544E-02 0.49164420E+00 0.66934114-154 0.66934114-154 0.49164420E+00 0.66905054-154 0.66905054-154
 IS,NS,NQ,X,H =    2 4014    5 0.72000000E+01 0.18092544E-02 0.48675226E+00 0.45100128-156 0.45100128-156 0.48675226E+00 0.45080271-156 0.45080271-156
 IS,NS,NQ,X,H =    2 4069    5 0.73000000E+01 0.18092544E-02 0.48190899E+00 0.30388414-158 0.30388414-158 0.48190899E+00 0.30374847-158 0.30374847-158
 IS,NS,NQ,X,H =    2 4124    5 0.74000000E+01 0.18092544E-02 0.47711392E+00 0.20475678-160 0.20475678-160 0.47711392E+00 0.20466411-160 0.20466411-160
 IS,NS,NQ,X,H =    2 4179    5 0.75000000E+01 0.18092544E-02 0.47236655E+00 0.13796488-162 0.13796488-162 0.47236655E+00 0.13790159-162 0.13790159-162
 IS,NS,NQ,X,H =    2 4235    5 0.76000000E+01 0.18092544E-02 0.46766643E+00 0.92960575-165 0.92960575-165 0.46766643E+00 0.92917363-165 0.92917363-165
 IS,NS,NQ,X,H =    2 4290    5 0.77000000E+01 0.18092544E-02 0.46301307E+00 0.62636728-167 0.62636728-167 0.46301307E+00 0.62607227-167 0.62607227-167
 IS,NS,NQ,X,H =    2 4345    5 0.78000000E+01 0.18092544E-02 0.45840601E+00 0.42204554-169 0.42204554-169 0.45840601E+00 0.42184418-169 0.42184418-169
 IS,NS,NQ,X,H =    2 4401    5 0.79000000E+01 0.18092544E-02 0.45384480E+00 0.28437379-171 0.28437379-171 0.45384480E+00 0.28423637-171 0.28423637-171
 IS,NS,NQ,X,H =    2 4456    5 0.80000000E+01 0.18092544E-02 0.44932896E+00 0.19161073-173 0.19161073-173 0.44932896E+00 0.19151696-173 0.19151696-173
 IS,NS,NQ,X,H =    2 4511    5 0.81000000E+01 0.18092544E-02 0.44485807E+00 0.12910709-175 0.12910709-175 0.44485807E+00 0.12904311-175 0.12904311-175
 IS,NS,NQ,X,H =    2 4566    5 0.82000000E+01 0.18092544E-02 0.44043165E+00 0.86992206-178 0.86992206-178 0.44043165E+00 0.86948565-178 0.86948565-178
 IS,NS,NQ,X,H =    2 4622    5 0.83000000E+01 0.18092544E-02 0.43604929E+00 0.58615246-180 0.58615246-180 0.43604929E+00 0.58585482-180 0.58585482-180
 IS,NS,NQ,X,H =    2 4677    5 0.84000000E+01 0.18092544E-02 0.43171052E+00 0.39494885-182 0.39494885-182 0.43171052E+00 0.39474588-182 0.39474588-182
 IS,NS,NQ,X,H =    2 4732    5 0.85000000E+01 0.18092544E-02 0.42741493E+00 0.26611608-184 0.26611608-184 0.42741493E+00 0.26597768-184 0.26597768-184
 IS,NS,NQ,X,H =    2 4787    5 0.86000000E+01 0.18092544E-02 0.42316208E+00 0.17930870-186 0.17930870-186 0.42316208E+00 0.17921435-186 0.17921435-186
 IS,NS,NQ,X,H =    2 4843    5 0.87000000E+01 0.18092544E-02 0.41895155E+00 0.12081799-188 0.12081799-188 0.41895155E+00 0.12075368-188 0.12075368-188
 IS,NS,NQ,X,H =    2 4898    5 0.88000000E+01 0.18092544E-02 0.41478291E+00 0.81407024-191 0.81407024-191 0.41478291E+00 0.81363189-191 0.81363189-191
 IS,NS,NQ,X,H =    2 4953    5 0.89000000E+01 0.18092544E-02 0.41065575E+00 0.54851959-193 0.54851959-193 0.41065575E+00 0.54822086-193 0.54822086-193
 IS,NS,NQ,X,H =    2 5008    5 0.90000000E+01 0.18092544E-02 0.40656966E+00 0.36959185-195 0.36959185-195 0.40656966E+00 0.36938831-195 0.36938831-195
 IS,NS,NQ,X,H =    2 5064    5 0.91000000E+01 0.18092544E-02 0.40252422E+00 0.24903056-197 0.24903056-197 0.40252422E+00 0.24889188-197 0.24889188-197
 IS,NS,NQ,X,H =    2 5119    5 0.92000000E+01 0.18092544E-02 0.39851904E+00 0.16779650-199 0.16779650-199 0.39851904E+00 0.16770203-199 0.16770203-199
 IS,NS,NQ,X,H =    2 5174    5 0.93000000E+01 0.18092544E-02 0.39455371E+00 0.11306109-201 0.11306109-201 0.39455371E+00 0.11299674-201 0.11299674-201
 IS,NS,NQ,X,H =    2 5230    5 0.94000000E+01 0.18092544E-02 0.39062784E+00 0.76180429-204 0.76180429-204 0.39062784E+00 0.76136605-204 0.76136605-204
 IS,NS,NQ,X,H =    2 5285    5 0.95000000E+01 0.18092544E-02 0.38674102E+00 0.51330285-206 0.51330285-206 0.38674102E+00 0.51300441-206 0.51300441-206
 IS,NS,NQ,X,H =    2 5340    5 0.96000000E+01 0.18092544E-02 0.38289289E+00 0.34586286-208 0.34586286-208 0.38289289E+00 0.34565965-208 0.34565965-208
 IS,NS,NQ,X,H =    2 5395    5 0.97000000E+01 0.18092544E-02 0.37908304E+00 0.23304199-210 0.23304199-210 0.37908304E+00 0.23290364-210 0.23290364-210
 IS,NS,NQ,X,H =    2 5451    5 0.98000000E+01 0.18092544E-02 0.37531110E+00 0.15702342-212 0.15702342-212 0.37531110E+00 0.15692924-212 0.15692924-212
 IS,NS,NQ,X,H =    2 5506    5 0.99000000E+01 0.18092544E-02 0.37157669E+00 0.10580220-214 0.10580220-214 0.37157669E+00 0.10573809-214 0.10573809-214
 IS,NS,NQ,X,H =    2 5561    5 0.10000000E+02 0.18092544E-02 0.36787944E+00 0.71289400-217 0.71289400-217 0.36787944E+00 0.71245764-217 0.71245764-217
   CPU(SEC) =            0.20

同様に、VODEのAdams法（MF=10）のときの、出力をリスト５に示す。BDF法と比較して数値解との相対誤差が0.1%程度とやや大きいが、正常な解が得られている。例題１でAdams法で解けるということは、Stiffnessがまだ小さいということか。

リスト５：VODEのAdams法による出力


 isw,ind =     1   13
  ----- nonstiff(Adams) by VODE.for -----
                  IS   NS   NQ           X              H              Y(1)           Y(2)           Y(3)        YANA(1)        YANA(2)        YANA(3)
 IS,NS,NQ,X,H =    1    0    0 0.00000000E+00 0.00000000E+00 0.20000000E+01 0.10000000E+01 0.20000000E+01 0.20000000E+01 0.10000000E+01 0.20000000E+01
 IS,NS,NQ,X,H =    2   65    5 0.10000000E+00 0.31624258E-02 0.99678779E+00 0.67379592E-02 0.67441008E-02 0.99678778E+00 0.67379470E-02 0.67440912E-02
 IS,NS,NQ,X,H =    2   97    5 0.20000000E+00 0.31624258E-02 0.98024407E+00 0.45400410E-04 0.45400447E-04 0.98024407E+00 0.45399930E-04 0.45399968E-04
 IS,NS,NQ,X,H =    2  129    5 0.30000000E+00 0.31624258E-02 0.97044584E+00 0.30590830E-06 0.30590830E-06 0.97044584E+00 0.30590232E-06 0.30590232E-06
 IS,NS,NQ,X,H =    2  160    5 0.40000000E+00 0.31624258E-02 0.96078944E+00 0.20612123E-08 0.20612123E-08 0.96078944E+00 0.20611536E-08 0.20611536E-08
 IS,NS,NQ,X,H =    2  192    5 0.50000000E+00 0.31624258E-02 0.95122942E+00 0.13888463E-10 0.13888463E-10 0.95122942E+00 0.13887944E-10 0.13887944E-10
 IS,NS,NQ,X,H =    2  223    5 0.60000000E+00 0.31624258E-02 0.94176453E+00 0.93580568E-13 0.93580568E-13 0.94176453E+00 0.93576230E-13 0.93576230E-13
 IS,NS,NQ,X,H =    2  255    5 0.70000000E+00 0.31624258E-02 0.93239382E+00 0.63054650E-15 0.63054650E-15 0.93239382E+00 0.63051168E-15 0.63051168E-15
 IS,NS,NQ,X,H =    2  287    5 0.80000000E+00 0.31624258E-02 0.92311635E+00 0.42486268E-17 0.42486268E-17 0.92311635E+00 0.42483543E-17 0.42483543E-17
 IS,NS,NQ,X,H =    2  318    5 0.90000000E+00 0.31624258E-02 0.91393119E+00 0.28627280E-19 0.28627280E-19 0.91393119E+00 0.28625186E-19 0.28625186E-19
 IS,NS,NQ,X,H =    2  350    5 0.10000000E+01 0.31624258E-02 0.90483742E+00 0.19289080E-21 0.19289080E-21 0.90483742E+00 0.19287498E-21 0.19287498E-21
 IS,NS,NQ,X,H =    2  382    5 0.11000000E+01 0.31624258E-02 0.89583414E+00 0.12996997E-23 0.12996997E-23 0.89583414E+00 0.12995814E-23 0.12995814E-23
 IS,NS,NQ,X,H =    2  413    5 0.12000000E+01 0.31624258E-02 0.88692044E+00 0.87573856E-26 0.87573856E-26 0.88692044E+00 0.87565108E-26 0.87565108E-26
 IS,NS,NQ,X,H =    2  445    5 0.13000000E+01 0.31624258E-02 0.87809543E+00 0.59007325E-28 0.59007325E-28 0.87809543E+00 0.59000905E-28 0.59000905E-28
 IS,NS,NQ,X,H =    2  476    5 0.14000000E+01 0.31624258E-02 0.86935824E+00 0.39759181E-30 0.39759181E-30 0.86935824E+00 0.39754497E-30 0.39754497E-30
 IS,NS,NQ,X,H =    2  508    5 0.15000000E+01 0.31624258E-02 0.86070798E+00 0.26789763E-32 0.26789763E-32 0.86070798E+00 0.26786370E-32 0.26786370E-32
 IS,NS,NQ,X,H =    2  540    5 0.16000000E+01 0.31624258E-02 0.85214379E+00 0.18050961E-34 0.18050961E-34 0.85214379E+00 0.18048514E-34 0.18048514E-34
 IS,NS,NQ,X,H =    2  571    5 0.17000000E+01 0.31624258E-02 0.84366482E+00 0.12162751E-36 0.12162751E-36 0.84366482E+00 0.12160993E-36 0.12160993E-36
 IS,NS,NQ,X,H =    2  603    5 0.18000000E+01 0.31624258E-02 0.83527021E+00 0.81952700E-39 0.81952700E-39 0.83527021E+00 0.81940126E-39 0.81940126E-39
 IS,NS,NQ,X,H =    2  634    5 0.19000000E+01 0.31624258E-02 0.82695913E+00 0.55219791E-41 0.55219791E-41 0.82695913E+00 0.55210823E-41 0.55210823E-41
 IS,NS,NQ,X,H =    2  666    5 0.20000000E+01 0.31624258E-02 0.81873075E+00 0.37207134E-43 0.37207134E-43 0.81873075E+00 0.37200760E-43 0.37200760E-43
 IS,NS,NQ,X,H =    2  698    5 0.21000000E+01 0.31624258E-02 0.81058425E+00 0.25070193E-45 0.25070193E-45 0.81058425E+00 0.25065675E-45 0.25065675E-45
 IS,NS,NQ,X,H =    2  729    5 0.22000000E+01 0.31624258E-02 0.80251880E+00 0.16892315E-47 0.16892315E-47 0.80251880E+00 0.16889119E-47 0.16889119E-47
 IS,NS,NQ,X,H =    2  761    5 0.23000000E+01 0.31624258E-02 0.79453360E+00 0.11382053E-49 0.11382053E-49 0.79453360E+00 0.11379799E-49 0.11379799E-49
 IS,NS,NQ,X,H =    2  793    5 0.24000000E+01 0.31624258E-02 0.78662786E+00 0.76692357E-52 0.76692357E-52 0.78662786E+00 0.76676481E-52 0.76676481E-52
 IS,NS,NQ,X,H =    2  824    5 0.25000000E+01 0.31624258E-02 0.77880078E+00 0.51675367E-54 0.51675367E-54 0.77880078E+00 0.51664206E-54 0.51664206E-54
 IS,NS,NQ,X,H =    2  856    5 0.26000000E+01 0.31624258E-02 0.77105159E+00 0.34818897E-56 0.34818897E-56 0.77105159E+00 0.34811068E-56 0.34811068E-56
 IS,NS,NQ,X,H =    2  887    5 0.27000000E+01 0.31624258E-02 0.76337949E+00 0.23461000E-58 0.23461000E-58 0.76337949E+00 0.23455513E-58 0.23455513E-58
 IS,NS,NQ,X,H =    2  919    5 0.28000000E+01 0.31624258E-02 0.75578374E+00 0.15808038E-60 0.15808038E-60 0.75578374E+00 0.15804201E-60 0.15804201E-60
 IS,NS,NQ,X,H =    2  951    5 0.29000000E+01 0.31624258E-02 0.74826357E+00 0.10651467E-62 0.10651467E-62 0.74826357E+00 0.10648787E-62 0.10648787E-62
 IS,NS,NQ,X,H =    2  982    5 0.30000000E+01 0.31624258E-02 0.74081822E+00 0.71769665E-65 0.71769665E-65 0.74081822E+00 0.71750960E-65 0.71750960E-65
 IS,NS,NQ,X,H =    2 1014    5 0.31000000E+01 0.31624258E-02 0.73344696E+00 0.48358448E-67 0.48358448E-67 0.73344696E+00 0.48345416E-67 0.48345416E-67
 IS,NS,NQ,X,H =    2 1046    5 0.32000000E+01 0.31624258E-02 0.72614904E+00 0.32583958E-69 0.32583958E-69 0.72614904E+00 0.32574885E-69 0.32574885E-69
 IS,NS,NQ,X,H =    2 1077    5 0.33000000E+01 0.31624258E-02 0.71892373E+00 0.21955095E-71 0.21955095E-71 0.71892373E+00 0.21948785E-71 0.21948785E-71
 IS,NS,NQ,X,H =    2 1109    5 0.34000000E+01 0.31624258E-02 0.71177032E+00 0.14793358E-73 0.14793358E-73 0.71177032E+00 0.14788975E-73 0.14788975E-73
 IS,NS,NQ,X,H =    2 1140    5 0.35000000E+01 0.31624258E-02 0.70468809E+00 0.99677758E-76 0.99677758E-76 0.70468809E+00 0.99647330E-76 0.99647330E-76
 IS,NS,NQ,X,H =    2 1172    5 0.36000000E+01 0.31624258E-02 0.69767633E+00 0.67162941E-78 0.67162941E-78 0.69767633E+00 0.67141843E-78 0.67141843E-78
 IS,NS,NQ,X,H =    2 1204    5 0.37000000E+01 0.31624258E-02 0.69073433E+00 0.45254437E-80 0.45254437E-80 0.69073433E+00 0.45239818E-80 0.45239818E-80
 IS,NS,NQ,X,H =    2 1235    5 0.38000000E+01 0.31624258E-02 0.68386141E+00 0.30492474E-82 0.30492474E-82 0.68386141E+00 0.30482350E-82 0.30482350E-82
 IS,NS,NQ,X,H =    2 1267    5 0.39000000E+01 0.31624258E-02 0.67705687E+00 0.20545849E-84 0.20545849E-84 0.67705687E+00 0.20538846E-84 0.20538846E-84
 IS,NS,NQ,X,H =    2 1299    5 0.40000000E+01 0.31624258E-02 0.67032005E+00 0.13843809E-86 0.13843809E-86 0.67032005E+00 0.13838965E-86 0.13838965E-86
 IS,NS,NQ,X,H =    2 1330    5 0.41000000E+01 0.31624258E-02 0.66365025E+00 0.93279682E-89 0.93279682E-89 0.66365025E+00 0.93246214E-89 0.93246214E-89
 IS,NS,NQ,X,H =    2 1362    5 0.42000000E+01 0.31624258E-02 0.65704682E+00 0.62851914E-91 0.62851914E-91 0.65704682E+00 0.62828805E-91 0.62828805E-91
 IS,NS,NQ,X,H =    2 1393    5 0.43000000E+01 0.31624258E-02 0.65050909E+00 0.42349668E-93 0.42349668E-93 0.65050909E+00 0.42333716E-93 0.42333716E-93
 IS,NS,NQ,X,H =    2 1425    5 0.44000000E+01 0.31624258E-02 0.64403642E+00 0.28535235E-95 0.28535235E-95 0.64403642E+00 0.28524233E-95 0.28524233E-95
 IS,NS,NQ,X,H =    2 1457    5 0.45000000E+01 0.31624258E-02 0.63762815E+00 0.19227062E-97 0.19227062E-97 0.63762815E+00 0.19219477E-97 0.19219477E-97
 IS,NS,NQ,X,H =    2 1488    5 0.46000000E+01 0.31624258E-02 0.63128365E+00 0.12955209E-99 0.12955209E-99 0.63128365E+00 0.12949982E-99 0.12949982E-99
 IS,NS,NQ,X,H =    2 1520    5 0.47000000E+01 0.31624258E-02 0.62500227E+00 0.87292282-102 0.87292282-102 0.62500227E+00 0.87256292-102 0.87256292-102
 IS,NS,NQ,X,H =    2 1552    5 0.48000000E+01 0.31624258E-02 0.61878339E+00 0.58817605-104 0.58817605-104 0.61878339E+00 0.58792827-104 0.58792827-104
 IS,NS,NQ,X,H =    2 1583    5 0.49000000E+01 0.31624258E-02 0.61262639E+00 0.39631344-106 0.39631344-106 0.61262639E+00 0.39614295-106 0.39614295-106
 IS,NS,NQ,X,H =    2 1615    5 0.50000000E+01 0.31624258E-02 0.60653066E+00 0.26703627-108 0.26703627-108 0.60653066E+00 0.26691902-108 0.26691902-108
 IS,NS,NQ,X,H =    2 1646    5 0.51000000E+01 0.31624258E-02 0.60049558E+00 0.17992924-110 0.17992924-110 0.60049558E+00 0.17984862-110 0.17984862-110
 IS,NS,NQ,X,H =    2 1678    5 0.52000000E+01 0.31624258E-02 0.59452055E+00 0.12123645-112 0.12123645-112 0.59452055E+00 0.12118105-112 0.12118105-112
 IS,NS,NQ,X,H =    2 1710    5 0.53000000E+01 0.31624258E-02 0.58860497E+00 0.81689205-115 0.81689205-115 0.58860497E+00 0.81651148-115 0.81651148-115
 IS,NS,NQ,X,H =    2 1741    5 0.54000000E+01 0.31624258E-02 0.58274825E+00 0.55042247-117 0.55042247-117 0.58274825E+00 0.55016111-117 0.55016111-117
 IS,NS,NQ,X,H =    2 1773    5 0.55000000E+01 0.31624258E-02 0.57694981E+00 0.37087503-119 0.37087503-119 0.57694981E+00 0.37069564-119 0.37069564-119
 IS,NS,NQ,X,H =    2 1804    5 0.56000000E+01 0.31624258E-02 0.57120906E+00 0.24989588-121 0.24989588-121 0.57120906E+00 0.24977276-121 0.24977276-121
 IS,NS,NQ,X,H =    2 1836    5 0.57000000E+01 0.31624258E-02 0.56552544E+00 0.16838002-123 0.16838002-123 0.56552544E+00 0.16829556-123 0.16829556-123
 IS,NS,NQ,X,H =    2 1868    5 0.58000000E+01 0.31624258E-02 0.55989837E+00 0.11345457-125 0.11345457-125 0.55989837E+00 0.11339666-125 0.11339666-125
 IS,NS,NQ,X,H =    2 1899    5 0.59000000E+01 0.31624258E-02 0.55432728E+00 0.76445777-128 0.76445777-128 0.55432728E+00 0.76406066-128 0.76406066-128
 IS,NS,NQ,X,H =    2 1931    5 0.60000000E+01 0.31624258E-02 0.54881164E+00 0.51509216-130 0.51509216-130 0.54881164E+00 0.51482002-130 0.51482002-130
 IS,NS,NQ,X,H =    2 1963    5 0.61000000E+01 0.31624258E-02 0.54335087E+00 0.34706947-132 0.34706947-132 0.54335087E+00 0.34688300-132 0.34688300-132
 IS,NS,NQ,X,H =    2 1994    5 0.62000000E+01 0.31624258E-02 0.53794444E+00 0.23385567-134 0.23385567-134 0.53794444E+00 0.23372793-134 0.23372793-134
 IS,NS,NQ,X,H =    2 2026    5 0.63000000E+01 0.31624258E-02 0.53259180E+00 0.15757211-136 0.15757211-136 0.53259180E+00 0.15748464-136 0.15748464-136
 IS,NS,NQ,X,H =    2 2057    5 0.64000000E+01 0.31624258E-02 0.52729242E+00 0.10617221-138 0.10617221-138 0.52729242E+00 0.10611232-138 0.10611232-138
 IS,NS,NQ,X,H =    2 2089    5 0.65000000E+01 0.31624258E-02 0.52204578E+00 0.71538905-141 0.71538905-141 0.52204578E+00 0.71497916-141 0.71497916-141
 IS,NS,NQ,X,H =    2 2121    5 0.66000000E+01 0.31624258E-02 0.51685133E+00 0.48202965-143 0.48202965-143 0.51685133E+00 0.48174917-143 0.48174917-143
 IS,NS,NQ,X,H =    2 2152    5 0.67000000E+01 0.31624258E-02 0.51170858E+00 0.32479194-145 0.32479194-145 0.51170858E+00 0.32460004-145 0.32460004-145
 IS,NS,NQ,X,H =    2 2184    5 0.68000000E+01 0.31624258E-02 0.50661699E+00 0.21884503-147 0.21884503-147 0.50661699E+00 0.21871378-147 0.21871378-147
 IS,NS,NQ,X,H =    2 2216    5 0.69000000E+01 0.31624258E-02 0.50157607E+00 0.14745794-149 0.14745794-149 0.50157607E+00 0.14736819-149 0.14736819-149
 IS,NS,NQ,X,H =    2 2247    5 0.70000000E+01 0.31624258E-02 0.49658530E+00 0.99357268-152 0.99357268-152 0.49658530E+00 0.99295904-152 0.99295904-152
 IS,NS,NQ,X,H =    2 2279    5 0.71000000E+01 0.31624258E-02 0.49164420E+00 0.66946995-154 0.66946995-154 0.49164420E+00 0.66905054-154 0.66905054-154
 IS,NS,NQ,X,H =    2 2310    5 0.72000000E+01 0.31624258E-02 0.48675226E+00 0.45108937-156 0.45108937-156 0.48675226E+00 0.45080271-156 0.45080271-156
 IS,NS,NQ,X,H =    2 2342    5 0.73000000E+01 0.31624258E-02 0.48190899E+00 0.30394432-158 0.30394432-158 0.48190899E+00 0.30374847-158 0.30374847-158
 IS,NS,NQ,X,H =    2 2374    5 0.74000000E+01 0.31624258E-02 0.47711392E+00 0.20479790-160 0.20479790-160 0.47711392E+00 0.20466411-160 0.20466411-160
 IS,NS,NQ,X,H =    2 2405    5 0.75000000E+01 0.31624258E-02 0.47236655E+00 0.13799298-162 0.13799298-162 0.47236655E+00 0.13790159-162 0.13790159-162
 IS,NS,NQ,X,H =    2 2437    5 0.76000000E+01 0.31624258E-02 0.46766643E+00 0.92979762-165 0.92979762-165 0.46766643E+00 0.92917363-165 0.92917363-165
 IS,NS,NQ,X,H =    2 2469    5 0.77000000E+01 0.31624258E-02 0.46301307E+00 0.62649833-167 0.62649833-167 0.46301307E+00 0.62607227-167 0.62607227-167
 IS,NS,NQ,X,H =    2 2500    5 0.78000000E+01 0.31624258E-02 0.45840601E+00 0.42213502-169 0.42213502-169 0.45840601E+00 0.42184418-169 0.42184418-169
 IS,NS,NQ,X,H =    2 2532    5 0.79000000E+01 0.31624258E-02 0.45384480E+00 0.28443487-171 0.28443487-171 0.45384480E+00 0.28423637-171 0.28423637-171
 IS,NS,NQ,X,H =    2 2563    5 0.80000000E+01 0.31624258E-02 0.44932896E+00 0.19165243-173 0.19165243-173 0.44932896E+00 0.19151696-173 0.19151696-173
 IS,NS,NQ,X,H =    2 2595    5 0.81000000E+01 0.31624258E-02 0.44485807E+00 0.12913554-175 0.12913554-175 0.44485807E+00 0.12904311-175 0.12904311-175
 IS,NS,NQ,X,H =    2 2627    5 0.82000000E+01 0.31624258E-02 0.44043165E+00 0.87011619-178 0.87011619-178 0.44043165E+00 0.86948565-178 0.86948565-178
 IS,NS,NQ,X,H =    2 2658    5 0.83000000E+01 0.31624258E-02 0.43604929E+00 0.58628494-180 0.58628494-180 0.43604929E+00 0.58585482-180 0.58585482-180
 IS,NS,NQ,X,H =    2 2690    5 0.84000000E+01 0.31624258E-02 0.43171052E+00 0.39503918-182 0.39503918-182 0.43171052E+00 0.39474588-182 0.39474588-182
 IS,NS,NQ,X,H =    2 2722    5 0.85000000E+01 0.31624258E-02 0.42741493E+00 0.26617770-184 0.26617770-184 0.42741493E+00 0.26597768-184 0.26597768-184
 IS,NS,NQ,X,H =    2 2753    5 0.86000000E+01 0.31624258E-02 0.42316208E+00 0.17935072-186 0.17935072-186 0.42316208E+00 0.17921435-186 0.17921435-186
 IS,NS,NQ,X,H =    2 2785    5 0.87000000E+01 0.31624258E-02 0.41895155E+00 0.12084664-188 0.12084664-188 0.41895155E+00 0.12075368-188 0.12075368-188
 IS,NS,NQ,X,H =    2 2816    5 0.88000000E+01 0.31624258E-02 0.41478291E+00 0.81426559-191 0.81426559-191 0.41478291E+00 0.81363189-191 0.81363189-191
 IS,NS,NQ,X,H =    2 2848    5 0.89000000E+01 0.31624258E-02 0.41065575E+00 0.54865270-193 0.54865270-193 0.41065575E+00 0.54822086-193 0.54822086-193
 IS,NS,NQ,X,H =    2 2880    5 0.90000000E+01 0.31624258E-02 0.40656966E+00 0.36968259-195 0.36968259-195 0.40656966E+00 0.36938831-195 0.36938831-195
 IS,NS,NQ,X,H =    2 2911    5 0.91000000E+01 0.31624258E-02 0.40252422E+00 0.24909240-197 0.24909240-197 0.40252422E+00 0.24889188-197 0.24889188-197
 IS,NS,NQ,X,H =    2 2943    5 0.92000000E+01 0.31624258E-02 0.39851904E+00 0.16783863-199 0.16783863-199 0.39851904E+00 0.16770203-199 0.16770203-199
 IS,NS,NQ,X,H =    2 2974    5 0.93000000E+01 0.31624258E-02 0.39455371E+00 0.11308980-201 0.11308980-201 0.39455371E+00 0.11299674-201 0.11299674-201
 IS,NS,NQ,X,H =    2 3006    5 0.94000000E+01 0.31624258E-02 0.39062784E+00 0.76199983-204 0.76199983-204 0.39062784E+00 0.76136605-204 0.76136605-204
 IS,NS,NQ,X,H =    2 3038    5 0.95000000E+01 0.31624258E-02 0.38674102E+00 0.51343602-206 0.51343602-206 0.38674102E+00 0.51300441-206 0.51300441-206
 IS,NS,NQ,X,H =    2 3069    5 0.96000000E+01 0.31624258E-02 0.38289289E+00 0.34595358-208 0.34595358-208 0.38289289E+00 0.34565965-208 0.34565965-208
 IS,NS,NQ,X,H =    2 3101    5 0.97000000E+01 0.31624258E-02 0.37908304E+00 0.23310375-210 0.23310375-210 0.37908304E+00 0.23290364-210 0.23290364-210
 IS,NS,NQ,X,H =    2 3133    5 0.98000000E+01 0.31624258E-02 0.37531110E+00 0.15706548-212 0.15706548-212 0.37531110E+00 0.15692924-212 0.15692924-212
 IS,NS,NQ,X,H =    2 3164    5 0.99000000E+01 0.31624258E-02 0.37157669E+00 0.10583084-214 0.10583084-214 0.37157669E+00 0.10573809-214 0.10573809-214
 IS,NS,NQ,X,H =    2 3196    5 0.10000000E+02 0.31624258E-02 0.36787944E+00 0.71308889-217 0.71308889-217 0.36787944E+00 0.71245764-217 0.71245764-217
   CPU(SEC) =            0.20

先頭に戻る

ODEPACKによる解

ODEPACKのGear法による計算結果をリスト６に示す。Gear法でほぼ正常に解けている。

リスト６：ODEPACKのGear法による出力


 isw,ind =     1    9
  ---- Gear Method (ODEPACK) ----
                  IS   NS   NQ           X              H              Y(1)           Y(2)           Y(3)        YANA(1)        YANA(2)        YANA(3)
 IS,NS,NQ,X,H =    1    0    0 0.00000000E+00 0.00000000E+00 0.20000000E+01 0.10000000E+01 0.20000000E+01 0.20000000E+01 0.10000000E+01 0.20000000E+01
 IS,NS,NQ,X,H =    2   82    5 0.10000000E+00 0.10000000E-04 0.99678781E+00 0.67379797E-02 0.67441323E-02 0.99678778E+00 0.67379470E-02 0.67440912E-02
 IS,NS,NQ,X,H =    2  128    5 0.20000000E+00 0.10000000E-04 0.98024407E+00 0.45400937E-04 0.45400975E-04 0.98024407E+00 0.45399930E-04 0.45399968E-04
 IS,NS,NQ,X,H =    2  173    5 0.30000000E+00 0.10000000E-04 0.97044584E+00 0.30591435E-06 0.30591435E-06 0.97044584E+00 0.30590232E-06 0.30590232E-06
 IS,NS,NQ,X,H =    2  219    5 0.40000000E+00 0.10000000E-04 0.96078944E+00 0.20612700E-08 0.20612700E-08 0.96078944E+00 0.20611536E-08 0.20611536E-08
 IS,NS,NQ,X,H =    2  264    5 0.50000000E+00 0.10000000E-04 0.95122942E+00 0.13888966E-10 0.13888966E-10 0.95122942E+00 0.13887944E-10 0.13887944E-10
 IS,NS,NQ,X,H =    2  309    5 0.60000000E+00 0.10000000E-04 0.94176453E+00 0.93584720E-13 0.93584720E-13 0.94176453E+00 0.93576230E-13 0.93576230E-13
 IS,NS,NQ,X,H =    2  355    5 0.70000000E+00 0.10000000E-04 0.93239382E+00 0.63057971E-15 0.63057971E-15 0.93239382E+00 0.63051168E-15 0.63051168E-15
 IS,NS,NQ,X,H =    2  400    5 0.80000000E+00 0.10000000E-04 0.92311635E+00 0.42488856E-17 0.42488856E-17 0.92311635E+00 0.42483543E-17 0.42483543E-17
 IS,NS,NQ,X,H =    2  446    5 0.90000000E+00 0.10000000E-04 0.91393119E+00 0.28629256E-19 0.28629256E-19 0.91393119E+00 0.28625186E-19 0.28625186E-19
 IS,NS,NQ,X,H =    2  491    5 0.10000000E+01 0.10000000E-04 0.90483742E+00 0.19290572E-21 0.19290572E-21 0.90483742E+00 0.19287498E-21 0.19287498E-21
 IS,NS,NQ,X,H =    2  536    5 0.11000000E+01 0.10000000E-04 0.89583414E+00 0.12998108E-23 0.12998108E-23 0.89583414E+00 0.12995814E-23 0.12995814E-23
 IS,NS,NQ,X,H =    2  582    5 0.12000000E+01 0.10000000E-04 0.88692044E+00 0.87582064E-26 0.87582064E-26 0.88692044E+00 0.87565108E-26 0.87565108E-26
 IS,NS,NQ,X,H =    2  627    5 0.13000000E+01 0.10000000E-04 0.87809543E+00 0.59013343E-28 0.59013343E-28 0.87809543E+00 0.59000905E-28 0.59000905E-28
 IS,NS,NQ,X,H =    2  673    5 0.14000000E+01 0.10000000E-04 0.86935824E+00 0.39763558E-30 0.39763558E-30 0.86935824E+00 0.39754497E-30 0.39754497E-30
 IS,NS,NQ,X,H =    2  718    5 0.15000000E+01 0.10000000E-04 0.86070798E+00 0.26792935E-32 0.26792935E-32 0.86070798E+00 0.26786370E-32 0.26786370E-32
 IS,NS,NQ,X,H =    2  763    5 0.16000000E+01 0.10000000E-04 0.85214379E+00 0.18053246E-34 0.18053246E-34 0.85214379E+00 0.18048514E-34 0.18048514E-34
 IS,NS,NQ,X,H =    2  809    5 0.17000000E+01 0.10000000E-04 0.84366482E+00 0.12164390E-36 0.12164390E-36 0.84366482E+00 0.12160993E-36 0.12160993E-36
 IS,NS,NQ,X,H =    2  854    5 0.18000000E+01 0.10000000E-04 0.83527021E+00 0.81964425E-39 0.81964425E-39 0.83527021E+00 0.81940126E-39 0.81940126E-39
 IS,NS,NQ,X,H =    2  900    5 0.19000000E+01 0.10000000E-04 0.82695913E+00 0.55228140E-41 0.55228140E-41 0.82695913E+00 0.55210823E-41 0.55210823E-41
 IS,NS,NQ,X,H =    2  945    5 0.20000000E+01 0.10000000E-04 0.81873075E+00 0.37213067E-43 0.37213067E-43 0.81873075E+00 0.37200760E-43 0.37200760E-43
 IS,NS,NQ,X,H =    2  990    5 0.21000000E+01 0.10000000E-04 0.81058425E+00 0.25074397E-45 0.25074397E-45 0.81058425E+00 0.25065675E-45 0.25065675E-45
 IS,NS,NQ,X,H =    2 1036    5 0.22000000E+01 0.10000000E-04 0.80251880E+00 0.16895285E-47 0.16895285E-47 0.80251880E+00 0.16889119E-47 0.16889119E-47
 IS,NS,NQ,X,H =    2 1081    5 0.23000000E+01 0.10000000E-04 0.79453360E+00 0.11384149E-49 0.11384149E-49 0.79453360E+00 0.11379799E-49 0.11379799E-49
 IS,NS,NQ,X,H =    2 1127    5 0.24000000E+01 0.10000000E-04 0.78662786E+00 0.76707106E-52 0.76707106E-52 0.78662786E+00 0.76676481E-52 0.76676481E-52
 IS,NS,NQ,X,H =    2 1172    5 0.25000000E+01 0.10000000E-04 0.77880078E+00 0.51685729E-54 0.51685729E-54 0.77880078E+00 0.51664206E-54 0.51664206E-54
 IS,NS,NQ,X,H =    2 1217    5 0.26000000E+01 0.10000000E-04 0.77105159E+00 0.34826167E-56 0.34826167E-56 0.77105159E+00 0.34811068E-56 0.34811068E-56
 IS,NS,NQ,X,H =    2 1263    5 0.27000000E+01 0.10000000E-04 0.76337949E+00 0.23466089E-58 0.23466089E-58 0.76337949E+00 0.23455513E-58 0.23455513E-58
 IS,NS,NQ,X,H =    2 1308    5 0.28000000E+01 0.10000000E-04 0.75578374E+00 0.15811598E-60 0.15811598E-60 0.75578374E+00 0.15804201E-60 0.15804201E-60
 IS,NS,NQ,X,H =    2 1354    5 0.29000000E+01 0.10000000E-04 0.74826357E+00 0.10653953E-62 0.10653953E-62 0.74826357E+00 0.10648787E-62 0.10648787E-62
 IS,NS,NQ,X,H =    2 1399    5 0.30000000E+01 0.10000000E-04 0.74081822E+00 0.71787004E-65 0.71787004E-65 0.74081822E+00 0.71750960E-65 0.71750960E-65
 IS,NS,NQ,X,H =    2 1444    5 0.31000000E+01 0.10000000E-04 0.73344696E+00 0.48370531E-67 0.48370531E-67 0.73344696E+00 0.48345416E-67 0.48345416E-67
 IS,NS,NQ,X,H =    2 1490    5 0.32000000E+01 0.10000000E-04 0.72614904E+00 0.32592366E-69 0.32592366E-69 0.72614904E+00 0.32574885E-69 0.32574885E-69
 IS,NS,NQ,X,H =    2 1535    5 0.33000000E+01 0.10000000E-04 0.71892373E+00 0.21960941E-71 0.21960941E-71 0.71892373E+00 0.21948785E-71 0.21948785E-71
 IS,NS,NQ,X,H =    2 1581    5 0.34000000E+01 0.10000000E-04 0.71177032E+00 0.14797418E-73 0.14797418E-73 0.71177032E+00 0.14788975E-73 0.14788975E-73
 IS,NS,NQ,X,H =    2 1626    5 0.35000000E+01 0.10000000E-04 0.70468809E+00 0.99705934E-76 0.99705934E-76 0.70468809E+00 0.99647330E-76 0.99647330E-76
 IS,NS,NQ,X,H =    2 1671    5 0.36000000E+01 0.10000000E-04 0.69767633E+00 0.67182481E-78 0.67182481E-78 0.69767633E+00 0.67141843E-78 0.67141843E-78
 IS,NS,NQ,X,H =    2 1717    5 0.37000000E+01 0.10000000E-04 0.69073433E+00 0.45267975E-80 0.45267975E-80 0.69073433E+00 0.45239818E-80 0.45239818E-80
 IS,NS,NQ,X,H =    2 1762    5 0.38000000E+01 0.10000000E-04 0.68386141E+00 0.30501846E-82 0.30501846E-82 0.68386141E+00 0.30482350E-82 0.30482350E-82
 IS,NS,NQ,X,H =    2 1808    5 0.39000000E+01 0.10000000E-04 0.67705687E+00 0.20552333E-84 0.20552333E-84 0.67705687E+00 0.20538846E-84 0.20538846E-84
 IS,NS,NQ,X,H =    2 1853    5 0.40000000E+01 0.10000000E-04 0.67032005E+00 0.13848291E-86 0.13848291E-86 0.67032005E+00 0.13838965E-86 0.13838965E-86
 IS,NS,NQ,X,H =    2 1898    5 0.41000000E+01 0.10000000E-04 0.66365025E+00 0.93310651E-89 0.93310651E-89 0.66365025E+00 0.93246214E-89 0.93246214E-89
 IS,NS,NQ,X,H =    2 1944    5 0.42000000E+01 0.10000000E-04 0.65704682E+00 0.62873299E-91 0.62873299E-91 0.65704682E+00 0.62828805E-91 0.62828805E-91
 IS,NS,NQ,X,H =    2 1989    5 0.43000000E+01 0.10000000E-04 0.65050909E+00 0.42364423E-93 0.42364423E-93 0.65050909E+00 0.42333716E-93 0.42333716E-93
 IS,NS,NQ,X,H =    2 2035    5 0.44000000E+01 0.10000000E-04 0.64403642E+00 0.28545412E-95 0.28545412E-95 0.64403642E+00 0.28524233E-95 0.28524233E-95
 IS,NS,NQ,X,H =    2 2080    5 0.45000000E+01 0.10000000E-04 0.63762815E+00 0.19234078E-97 0.19234078E-97 0.63762815E+00 0.19219477E-97 0.19219477E-97
 IS,NS,NQ,X,H =    2 2125    5 0.46000000E+01 0.10000000E-04 0.63128365E+00 0.12960042E-99 0.12960042E-99 0.63128365E+00 0.12949982E-99 0.12949982E-99
 IS,NS,NQ,X,H =    2 2171    5 0.47000000E+01 0.10000000E-04 0.62500227E+00 0.87325570-102 0.87325570-102 0.62500227E+00 0.87256292-102 0.87256292-102
 IS,NS,NQ,X,H =    2 2216    5 0.48000000E+01 0.10000000E-04 0.61878339E+00 0.58840517-104 0.58840517-104 0.61878339E+00 0.58792827-104 0.58792827-104
 IS,NS,NQ,X,H =    2 2262    5 0.49000000E+01 0.10000000E-04 0.61262639E+00 0.39647106-106 0.39647106-106 0.61262639E+00 0.39614295-106 0.39614295-106
 IS,NS,NQ,X,H =    2 2307    5 0.50000000E+01 0.10000000E-04 0.60653066E+00 0.26714469-108 0.26714469-108 0.60653066E+00 0.26691902-108 0.26691902-108
 IS,NS,NQ,X,H =    2 2352    5 0.51000000E+01 0.10000000E-04 0.60049558E+00 0.18000376-110 0.18000376-110 0.60049558E+00 0.17984862-110 0.17984862-110
 IS,NS,NQ,X,H =    2 2398    5 0.52000000E+01 0.10000000E-04 0.59452055E+00 0.12128766-112 0.12128766-112 0.59452055E+00 0.12118105-112 0.12118105-112
 IS,NS,NQ,X,H =    2 2443    5 0.53000000E+01 0.10000000E-04 0.58860497E+00 0.81724384-115 0.81724384-115 0.58860497E+00 0.81651148-115 0.81651148-115
 IS,NS,NQ,X,H =    2 2489    5 0.54000000E+01 0.10000000E-04 0.58274825E+00 0.55066398-117 0.55066398-117 0.58274825E+00 0.55016111-117 0.55016111-117
 IS,NS,NQ,X,H =    2 2534    5 0.55000000E+01 0.10000000E-04 0.57694981E+00 0.37104085-119 0.37104085-119 0.57694981E+00 0.37069564-119 0.37069564-119
 IS,NS,NQ,X,H =    2 2579    5 0.56000000E+01 0.10000000E-04 0.57120906E+00 0.25000964-121 0.25000964-121 0.57120906E+00 0.24977276-121 0.24977276-121
 IS,NS,NQ,X,H =    2 2625    5 0.57000000E+01 0.10000000E-04 0.56552544E+00 0.16845806-123 0.16845806-123 0.56552544E+00 0.16829556-123 0.16829556-123
 IS,NS,NQ,X,H =    2 2670    5 0.58000000E+01 0.10000000E-04 0.55989837E+00 0.11350810-125 0.11350810-125 0.55989837E+00 0.11339666-125 0.11339666-125
 IS,NS,NQ,X,H =    2 2716    5 0.59000000E+01 0.10000000E-04 0.55432728E+00 0.76482460-128 0.76482460-128 0.55432728E+00 0.76406066-128 0.76406066-128
 IS,NS,NQ,X,H =    2 2761    5 0.60000000E+01 0.10000000E-04 0.54881164E+00 0.51534362-130 0.51534362-130 0.54881164E+00 0.51482002-130 0.51482002-130
 IS,NS,NQ,X,H =    2 2806    5 0.61000000E+01 0.10000000E-04 0.54335087E+00 0.34724175-132 0.34724175-132 0.54335087E+00 0.34688300-132 0.34688300-132
 IS,NS,NQ,X,H =    2 2852    5 0.62000000E+01 0.10000000E-04 0.53794444E+00 0.23397366-134 0.23397366-134 0.53794444E+00 0.23372793-134 0.23372793-134
 IS,NS,NQ,X,H =    2 2897    5 0.63000000E+01 0.10000000E-04 0.53259180E+00 0.15765292-136 0.15765292-136 0.53259180E+00 0.15748464-136 0.15748464-136
 IS,NS,NQ,X,H =    2 2943    5 0.64000000E+01 0.10000000E-04 0.52729242E+00 0.10622752-138 0.10622752-138 0.52729242E+00 0.10611232-138 0.10611232-138
 IS,NS,NQ,X,H =    2 2988    5 0.65000000E+01 0.10000000E-04 0.52204578E+00 0.71576768-141 0.71576768-141 0.52204578E+00 0.71497916-141 0.71497916-141
 IS,NS,NQ,X,H =    2 3033    5 0.66000000E+01 0.10000000E-04 0.51685133E+00 0.48228874-143 0.48228874-143 0.51685133E+00 0.48174917-143 0.48174917-143
 IS,NS,NQ,X,H =    2 3079    5 0.67000000E+01 0.10000000E-04 0.51170858E+00 0.32496916-145 0.32496916-145 0.51170858E+00 0.32460004-145 0.32460004-145
 IS,NS,NQ,X,H =    2 3124    5 0.68000000E+01 0.10000000E-04 0.50661699E+00 0.21896626-147 0.21896626-147 0.50661699E+00 0.21871378-147 0.21871378-147
 IS,NS,NQ,X,H =    2 3169    5 0.69000000E+01 0.10000000E-04 0.50157607E+00 0.14754083-149 0.14754083-149 0.50157607E+00 0.14736819-149 0.14736819-149
 IS,NS,NQ,X,H =    2 3215    5 0.70000000E+01 0.10000000E-04 0.49658530E+00 0.99413934-152 0.99413934-152 0.49658530E+00 0.99295904-152 0.99295904-152
 IS,NS,NQ,X,H =    2 3260    5 0.71000000E+01 0.10000000E-04 0.49164420E+00 0.66985731-154 0.66985731-154 0.49164420E+00 0.66905054-154 0.66905054-154
 IS,NS,NQ,X,H =    2 3306    5 0.72000000E+01 0.10000000E-04 0.48675226E+00 0.45135403-156 0.45135403-156 0.48675226E+00 0.45080271-156 0.45080271-156
 IS,NS,NQ,X,H =    2 3351    5 0.73000000E+01 0.10000000E-04 0.48190899E+00 0.30412518-158 0.30412518-158 0.48190899E+00 0.30374847-158 0.30374847-158
 IS,NS,NQ,X,H =    2 3396    5 0.74000000E+01 0.10000000E-04 0.47711392E+00 0.20492144-160 0.20492144-160 0.47711392E+00 0.20466411-160 0.20466411-160
 IS,NS,NQ,X,H =    2 3442    5 0.75000000E+01 0.10000000E-04 0.47236655E+00 0.13807735-162 0.13807735-162 0.47236655E+00 0.13790159-162 0.13790159-162
 IS,NS,NQ,X,H =    2 3487    5 0.76000000E+01 0.10000000E-04 0.46766643E+00 0.93037382-165 0.93037382-165 0.46766643E+00 0.92917363-165 0.92917363-165
 IS,NS,NQ,X,H =    2 3533    5 0.77000000E+01 0.10000000E-04 0.46301307E+00 0.62689168-167 0.62689168-167 0.46301307E+00 0.62607227-167 0.62607227-167
 IS,NS,NQ,X,H =    2 3578    5 0.78000000E+01 0.10000000E-04 0.45840601E+00 0.42240354-169 0.42240354-169 0.45840601E+00 0.42184418-169 0.42184418-169
 IS,NS,NQ,X,H =    2 3623    5 0.79000000E+01 0.10000000E-04 0.45384480E+00 0.28461814-171 0.28461814-171 0.45384480E+00 0.28423637-171 0.28423637-171
 IS,NS,NQ,X,H =    2 3669    5 0.80000000E+01 0.10000000E-04 0.44932896E+00 0.19177748-173 0.19177748-173 0.44932896E+00 0.19151696-173 0.19151696-173
 IS,NS,NQ,X,H =    2 3714    5 0.81000000E+01 0.10000000E-04 0.44485807E+00 0.12922087-175 0.12922087-175 0.44485807E+00 0.12904311-175 0.12904311-175
 IS,NS,NQ,X,H =    2 3760    5 0.82000000E+01 0.10000000E-04 0.44043165E+00 0.87069827-178 0.87069827-178 0.44043165E+00 0.86948565-178 0.86948565-178
 IS,NS,NQ,X,H =    2 3805    5 0.83000000E+01 0.10000000E-04 0.43604929E+00 0.58668196-180 0.58668196-180 0.43604929E+00 0.58585482-180 0.58585482-180
 IS,NS,NQ,X,H =    2 3850    5 0.84000000E+01 0.10000000E-04 0.43171052E+00 0.39530996-182 0.39530996-182 0.43171052E+00 0.39474588-182 0.39474588-182
 IS,NS,NQ,X,H =    2 3896    5 0.85000000E+01 0.10000000E-04 0.42741493E+00 0.26636233-184 0.26636233-184 0.42741493E+00 0.26597768-184 0.26597768-184
 IS,NS,NQ,X,H =    2 3941    5 0.86000000E+01 0.10000000E-04 0.42316208E+00 0.17947660-186 0.17947660-186 0.42316208E+00 0.17921435-186 0.17921435-186
 IS,NS,NQ,X,H =    2 3987    5 0.87000000E+01 0.10000000E-04 0.41895155E+00 0.12093245-188 0.12093245-188 0.41895155E+00 0.12075368-188 0.12075368-188
 IS,NS,NQ,X,H =    2 4032    5 0.88000000E+01 0.10000000E-04 0.41478291E+00 0.81485046-191 0.81485046-191 0.41478291E+00 0.81363189-191 0.81363189-191
 IS,NS,NQ,X,H =    2 4077    5 0.89000000E+01 0.10000000E-04 0.41065575E+00 0.54905132-193 0.54905132-193 0.41065575E+00 0.54822086-193 0.54822086-193
 IS,NS,NQ,X,H =    2 4123    5 0.90000000E+01 0.10000000E-04 0.40656966E+00 0.36995421-195 0.36995421-195 0.40656966E+00 0.36938831-195 0.36938831-195
 IS,NS,NQ,X,H =    2 4168    5 0.91000000E+01 0.10000000E-04 0.40252422E+00 0.24927747-197 0.24927747-197 0.40252422E+00 0.24889188-197 0.24889188-197
 IS,NS,NQ,X,H =    2 4214    5 0.92000000E+01 0.10000000E-04 0.39851904E+00 0.16796471-199 0.16796471-199 0.39851904E+00 0.16770203-199 0.16770203-199
 IS,NS,NQ,X,H =    2 4259    5 0.93000000E+01 0.10000000E-04 0.39455371E+00 0.11317567-201 0.11317567-201 0.39455371E+00 0.11299674-201 0.11299674-201
 IS,NS,NQ,X,H =    2 4304    5 0.94000000E+01 0.10000000E-04 0.39062784E+00 0.76258476-204 0.76258476-204 0.39062784E+00 0.76136605-204 0.76136605-204
 IS,NS,NQ,X,H =    2 4350    5 0.95000000E+01 0.10000000E-04 0.38674102E+00 0.51383438-206 0.51383438-206 0.38674102E+00 0.51300441-206 0.51300441-206
 IS,NS,NQ,X,H =    2 4395    5 0.96000000E+01 0.10000000E-04 0.38289289E+00 0.34622482-208 0.34622482-208 0.38289289E+00 0.34565965-208 0.34565965-208
 IS,NS,NQ,X,H =    2 4441    5 0.97000000E+01 0.10000000E-04 0.37908304E+00 0.23328844-210 0.23328844-210 0.37908304E+00 0.23290364-210 0.23290364-210
 IS,NS,NQ,X,H =    2 4486    5 0.98000000E+01 0.10000000E-04 0.37531110E+00 0.15719122-212 0.15719122-212 0.37531110E+00 0.15692924-212 0.15692924-212
 IS,NS,NQ,X,H =    2 4531    5 0.99000000E+01 0.10000000E-04 0.37157669E+00 0.10591642-214 0.10591642-214 0.37157669E+00 0.10573809-214 0.10573809-214
 IS,NS,NQ,X,H =    2 4577    5 0.10000000E+02 0.10000000E-04 0.36787944E+00 0.71367147-217 0.71367147-217 0.36787944E+00 0.71245764-217 0.71245764-217
   CPU(SEC) =            0.10

先頭に戻る

IMSLのGear法による解

IMSLのGear法による計算結果（途中まで）をリスト７に示す。Y(2),Y(3)の解が途中で不安定となり振動していることがわかる。

リスト７：IMSLのGear法による出力


 isw,ind =     1    6
 ---- APPLY Gear Method ----
                  IS   NS   NQ           X              H              Y(1)           Y(2)           Y(3)        YANA(1)        YANA(2)        YANA(3)
 NS,NF,ID,X,H =    0    0    0 0.00000000E+00 0.00000000E+00 0.20000000E+01 0.10000000E+01 0.20000000E+01 0.20000000E+01 0.10000000E+01 0.20000000E+01
 NS,NF,ID,X,H =   71  108    2 0.10000000E+00 0.37023755E-02 0.99678836E+00 0.67385268E-02 0.67448960E-02 0.99678778E+00 0.67379470E-02 0.67440912E-02
 NS,NF,ID,X,H =   88  125    2 0.20000000E+00 0.95050752E-02 0.98024452E+00 0.45844832E-04 0.45848269E-04 0.98024407E+00 0.45399930E-04 0.45399968E-04
 NS,NF,ID,X,H =   97  134    2 0.30000000E+00 0.14693672E-01 0.97044597E+00 0.43519384E-06 0.43527354E-06 0.97044584E+00 0.30590232E-06 0.30590232E-06
 NS,NF,ID,X,H =  102  139    2 0.40000000E+00 0.38880563E-01 0.96078954E+00 0.97471924E-07 0.10575727E-06 0.96078944E+00 0.20611536E-08 0.20611536E-08
 NS,NF,ID,X,H =  104  141    2 0.50000000E+00 0.38880563E-01 0.95122941E+00-0.19019194E-07-0.20578623E-07 0.95122942E+00 0.13887944E-10 0.13887944E-10
 NS,NF,ID,X,H =  107  144    2 0.60000000E+00 0.10230378E+00 0.94176456E+00 0.27684438E-07 0.30095642E-07 0.94176453E+00 0.93576230E-13 0.93576230E-13
 NS,NF,ID,X,H =  108  145    2 0.70000000E+00 0.10230378E+00 0.93239388E+00 0.62868734E-07 0.65811705E-07 0.93239382E+00 0.63051168E-15 0.63051168E-15
 NS,NF,ID,X,H =  109  146    2 0.80000000E+00 0.10230378E+00 0.92311637E+00 0.25716303E-07 0.26311986E-07 0.92311635E+00 0.42483543E-17 0.42483543E-17
 NS,NF,ID,X,H =  110  147    2 0.90000000E+00 0.10230378E+00 0.91393119E+00-0.96089000E-09-0.10965383E-08 0.91393119E+00 0.28625186E-19 0.28625186E-19
 NS,NF,ID,X,H =  111  148    2 0.10000000E+01 0.10230378E+00 0.90483742E+00-0.33298516E-08-0.33655945E-08 0.90483742E+00 0.19287498E-21 0.19287498E-21
 NS,NF,ID,X,H =  111  148    2 0.11000000E+01 0.10230378E+00 0.89583414E+00-0.72292711E-10-0.50239871E-10 0.89583414E+00 0.12995814E-23 0.12995814E-23
 NS,NF,ID,X,H =  112  149    2 0.12000000E+01 0.30283764E+00 0.88692049E+00 0.15383221E-07 0.16122298E-07 0.88692044E+00 0.87565108E-26 0.87565108E-26
 NS,NF,ID,X,H =  112  149    2 0.13000000E+01 0.30283764E+00 0.87809553E+00 0.21939478E-07 0.22917687E-07 0.87809543E+00 0.59000905E-28 0.59000905E-28
 NS,NF,ID,X,H =  112  149    2 0.14000000E+01 0.30283764E+00 0.86935833E+00 0.70490205E-08 0.72240976E-08 0.86935824E+00 0.39754497E-30 0.39754497E-30
 NS,NF,ID,X,H =  113  150    2 0.15000000E+01 0.30283764E+00 0.86070813E+00 0.79777084E-08 0.81427149E-08 0.86070798E+00 0.26786370E-32 0.26786370E-32
 NS,NF,ID,X,H =  113  150    2 0.16000000E+01 0.30283764E+00 0.85214400E+00 0.71700067E-08 0.73126955E-08 0.85214379E+00 0.18048514E-34 0.18048514E-34
 NS,NF,ID,X,H =  113  150    2 0.17000000E+01 0.30283764E+00 0.84366505E+00 0.20782329E-08 0.21039454E-08 0.84366482E+00 0.12160993E-36 0.12160993E-36
 NS,NF,ID,X,H =  114  151    2 0.18000000E+01 0.30283764E+00 0.83527052E+00 0.12148017E-09 0.10571665E-09 0.83527021E+00 0.81940126E-39 0.81940126E-39
 NS,NF,ID,X,H =  114  151    2 0.19000000E+01 0.30283764E+00 0.82695951E+00-0.73605914E-09-0.76397880E-09 0.82695913E+00 0.55210823E-41 0.55210823E-41
 NS,NF,ID,X,H =  114  151    2 0.20000000E+01 0.30283764E+00 0.81873116E+00-0.36452977E-09-0.37191329E-09 0.81873075E+00 0.37200760E-43 0.37200760E-43
･･･
途中省略
･･･

 NS,NF,ID,X,H =  124  164    2 0.90000000E+01 0.95976433E+00 0.40656698E+00-0.11489298E-10-0.11206898E-10 0.40656966E+00 0.36938831-195 0.36938831-195
 NS,NF,ID,X,H =  124  164    2 0.91000000E+01 0.95976433E+00 0.40252150E+00-0.81018647E-11-0.78340297E-11 0.40252422E+00 0.24889188-197 0.24889188-197
 NS,NF,ID,X,H =  124  164    2 0.92000000E+01 0.95976433E+00 0.39851629E+00-0.36181208E-11-0.33745997E-11 0.39851904E+00 0.16770203-199 0.16770203-199
 NS,NF,ID,X,H =  124  164    2 0.93000000E+01 0.95976433E+00 0.39455096E+00 0.20953891E-11 0.23035496E-11 0.39455371E+00 0.11299674-201 0.11299674-201
 NS,NF,ID,X,H =  125  166    2 0.94000000E+01 0.95976433E+00 0.39062501E+00 0.49522402E-11 0.51407716E-11 0.39062784E+00 0.76136605-204 0.76136605-204
 NS,NF,ID,X,H =  125  166    2 0.95000000E+01 0.95976433E+00 0.38673811E+00 0.74413189E-11 0.76089301E-11 0.38674102E+00 0.51300441-206 0.51300441-206
 NS,NF,ID,X,H =  125  166    2 0.96000000E+01 0.95976433E+00 0.38288989E+00 0.96530220E-11 0.97973487E-11 0.38289289E+00 0.34565965-208 0.34565965-208
 NS,NF,ID,X,H =  125  166    2 0.97000000E+01 0.95976433E+00 0.37907996E+00 0.11460159E-10 0.11579193E-10 0.37908304E+00 0.23290364-210 0.23290364-210
 NS,NF,ID,X,H =  125  166    2 0.98000000E+01 0.95976433E+00 0.37530795E+00 0.12724993E-10 0.12817128E-10 0.37531110E+00 0.15692924-212 0.15692924-212
 NS,NF,ID,X,H =  125  166    2 0.99000000E+01 0.95976433E+00 0.37157347E+00 0.13299238E-10 0.13363325E-10 0.37157669E+00 0.10573809-214 0.10573809-214
 NS,NF,ID,X,H =  125  166    2 0.10000000E+02 0.95976433E+00 0.36787617E+00 0.13024061E-10 0.13059454E-10 0.36787944E+00 0.71245764-217 0.71245764-217
   CPU(SEC) =            0.30

IMSLのGear法については、条件設定をいろいろ試していないため、こうした振動が現れたのかも知れぬ。

先頭に戻る

Semi-Implicit Runge-Kutta (3step)法による解

Semi-implicit Runge-Kutta (3step)法による計算結果（途中まで）をリスト８に示す。Y(2),Y(3)の解が次第に解析解からずれて行くことがわかる。

リスト８：Semi-implicit Runge-Kutta (3step)法による出力


 isw,ind =     1    4
  ----- 3-Step Implicit RK -----
                           ITR  INQ           X              H              Y(1)           Y(2)           Y(3)        YANA(1)        YANA(2)        YANA(3)
           ITR,INQ,X,H =     0    0 0.00000000E+00 0.00000000E+00 0.20000000E+01 0.10000000E+01 0.20000000E+01 0.20000000E+01 0.10000000E+01 0.20000000E+01
           ITR,INQ,X,H =    10    3 0.10000000E+00 0.10000000E-01 0.99666636E+00 0.66165245E-02 0.66197220E-02 0.99678778E+00 0.67379470E-02 0.67440912E-02
           ITR,INQ,X,H =    20    3 0.20000000E+00 0.10000000E-01 0.98024245E+00 0.43778397E-04 0.43778407E-04 0.98024407E+00 0.45399930E-04 0.45399968E-04
           ITR,INQ,X,H =    30    3 0.30000000E+00 0.10000000E-01 0.97044582E+00 0.28966403E-06 0.28966403E-06 0.97044584E+00 0.30590232E-06 0.30590232E-06
           ITR,INQ,X,H =    40    3 0.40000000E+00 0.10000000E-01 0.96078944E+00 0.19145309E-08 0.19145309E-08 0.96078944E+00 0.20611536E-08 0.20611536E-08
           ITR,INQ,X,H =    50    3 0.50000000E+00 0.10000000E-01 0.95122942E+00 0.12633925E-10 0.12633925E-10 0.95122942E+00 0.13887944E-10 0.13887944E-10
           ITR,INQ,X,H =    60    3 0.60000000E+00 0.10000000E-01 0.94176453E+00 0.83370841E-13 0.83370841E-13 0.94176453E+00 0.93576230E-13 0.93576230E-13
           ITR,INQ,X,H =    70    3 0.70000000E+00 0.10000000E-01 0.93239382E+00 0.55016135E-15 0.55016135E-15 0.93239382E+00 0.63051168E-15 0.63051168E-15
           ITR,INQ,X,H =    80    3 0.80000000E+00 0.10000000E-01 0.92311635E+00 0.36304961E-17 0.36304961E-17 0.92311635E+00 0.42483543E-17 0.42483543E-17
           ITR,INQ,X,H =    90    3 0.90000000E+00 0.10000000E-01 0.91393119E+00 0.23957521E-19 0.23957521E-19 0.91393119E+00 0.28625186E-19 0.28625186E-19
           ITR,INQ,X,H =   100    3 0.10000000E+01 0.10000000E-01 0.90483742E+00 0.15809487E-21 0.15809487E-21 0.90483742E+00 0.19287498E-21 0.19287498E-21
           ITR,INQ,X,H =   110    3 0.11000000E+01 0.10000000E-01 0.89583414E+00 0.10432627E-23 0.10432627E-23 0.89583414E+00 0.12995814E-23 0.12995814E-23
           ITR,INQ,X,H =   120    3 0.12000000E+01 0.10000000E-01 0.88692044E+00 0.68844549E-26 0.68844549E-26 0.88692044E+00 0.87565108E-26 0.87565108E-26
           ITR,INQ,X,H =   130    3 0.13000000E+01 0.10000000E-01 0.87809543E+00 0.45430284E-28 0.45430284E-28 0.87809543E+00 0.59000905E-28 0.59000905E-28
           ITR,INQ,X,H =   140    3 0.14000000E+01 0.10000000E-01 0.86935824E+00 0.29979290E-30 0.29979290E-30 0.86935824E+00 0.39754497E-30 0.39754497E-30
           ITR,INQ,X,H =   150    3 0.15000000E+01 0.10000000E-01 0.86070798E+00 0.19783232E-32 0.19783232E-32 0.86070798E+00 0.26786370E-32 0.26786370E-32
           ITR,INQ,X,H =   160    3 0.16000000E+01 0.10000000E-01 0.85214379E+00 0.13054888E-34 0.13054888E-34 0.85214379E+00 0.18048514E-34 0.18048514E-34
           ITR,INQ,X,H =   170    3 0.17000000E+01 0.10000000E-01 0.84366482E+00 0.86148761E-37 0.86148761E-37 0.84366482E+00 0.12160993E-36 0.12160993E-36
           ITR,INQ,X,H =   180    3 0.18000000E+01 0.10000000E-01 0.83527021E+00 0.56849275E-39 0.56849275E-39 0.83527021E+00 0.81940126E-39 0.81940126E-39
           ITR,INQ,X,H =   190    3 0.19000000E+01 0.10000000E-01 0.82695913E+00 0.37514644E-41 0.37514644E-41 0.82695913E+00 0.55210823E-41 0.55210823E-41
           ITR,INQ,X,H =   200    3 0.20000000E+01 0.10000000E-01 0.81873075E+00 0.24755786E-43 0.24755786E-43 0.81873075E+00 0.37200760E-43 0.37200760E-43
･･･
途中省略
･･･

           ITR,INQ,X,H =   900    3 0.90000000E+01 0.10000000E-01 0.40656966E+00 0.57146473-196 0.57146473-196 0.40656966E+00 0.36938831-195 0.36938831-195
           ITR,INQ,X,H =   910    3 0.91000000E+01 0.10000000E-01 0.40252422E+00 0.37710764-198 0.37710764-198 0.40252422E+00 0.24889188-197 0.24889188-197
           ITR,INQ,X,H =   920    3 0.92000000E+01 0.10000000E-01 0.39851904E+00 0.24885205-200 0.24885205-200 0.39851904E+00 0.16770203-199 0.16770203-199
           ITR,INQ,X,H =   930    3 0.93000000E+01 0.10000000E-01 0.39455371E+00 0.16421662-202 0.16421662-202 0.39455371E+00 0.11299674-201 0.11299674-201
           ITR,INQ,X,H =   940    3 0.94000000E+01 0.10000000E-01 0.39062784E+00 0.10836599-204 0.10836599-204 0.39062784E+00 0.76136605-204 0.76136605-204
           ITR,INQ,X,H =   950    3 0.95000000E+01 0.10000000E-01 0.38674102E+00 0.71510351-207 0.71510351-207 0.38674102E+00 0.51300441-206 0.51300441-206
           ITR,INQ,X,H =   960    3 0.96000000E+01 0.10000000E-01 0.38289289E+00 0.47189438-209 0.47189438-209 0.38289289E+00 0.34565965-208 0.34565965-208
           ITR,INQ,X,H =   970    3 0.97000000E+01 0.10000000E-01 0.37908304E+00 0.31140150-211 0.31140150-211 0.37908304E+00 0.23290364-210 0.23290364-210
           ITR,INQ,X,H =   980    3 0.98000000E+01 0.10000000E-01 0.37531110E+00 0.20549279-213 0.20549279-213 0.37531110E+00 0.15692924-212 0.15692924-212
           ITR,INQ,X,H =   990    3 0.99000000E+01 0.10000000E-01 0.37157669E+00 0.13560400-215 0.13560400-215 0.37157669E+00 0.10573809-214 0.10573809-214
           ITR,INQ,X,H =  1000    3 0.10000000E+02 0.10000000E-01 0.36787944E+00 0.89484618-218 0.89484618-218 0.36787944E+00 0.71245764-217 0.71245764-217
   CPU(SEC) =            0.10

例題１では、Adams法でもある程度の精度を持って解くことができたが、IMSLのGear法では解くことができなかった。設定条件の与え方を変えてもそれほど改善しなかった。 Recipe 77に記載のRosenbrook、Bulirsh-Stoer法ともに解くことができていない。

このように連立微分方程式のStiffnessの強度によっても、解ける場合と解けない場合が見られる。

先頭に戻る

そのほかの例題

Stiffな連立微分方程式の例の紹介と、解析結果について簡単に解説する。

例題２：連立微分方程式の解法

次の例題２¹¹⁾は、上の14個の連立微分方程式の解法すべてで、正常に解けた例題である。係数行列の固有値は-1、-1000で固有値の最大値と最小値の比率は1000倍である。例題１に比べ比率は大きい。

例題２：スティッフな微分方程式の解

次の連立微分方程式をスティッフな解法を用いて、ステップ幅0.01とし、ステップ数100まで解きなさい。なお初期刻み幅を1.E-5とする。 \[ \left . \eqalign { \begin{align*} y_1' & = 998y_1+1998y_2 \\ y_2' & =-999y_1-1999y_2 \\ y_1(0) & =1 \\ y_2(0) & =0 \\ \end{align*} } \right . \tag{A.4} \] なお、解析解は次のとおり。 \[ \left . \eqalign { \begin{align*} y_1=2 \exp(-x) - \exp(-1000x) \\ y_2= - \exp(-x) + \exp(-1000x) \\ \end{align*} } \right . \tag{A.5} \]

計算結果は掲載しない。各自で確認されたい。

例題１の計算と比べると、IMSLのGear法でも収束していることから、問題により得手不得手が解法にはあるらしい。

先頭に戻る

例題３¹¹⁾：連立微分方程式の解法

図書¹¹⁾にあるサンプルで、連立微分方程式の右辺が非線形となる例題である。

例題３：スティッフな微分方程式の解

次の連立微分方程式を初期条件の下で、\( 0 \gt t \gt 100 \) の範囲で、ステップ幅1.0とし、ステップ数100まで解きなさい。なお初期刻み幅を1.E-5とする。 \[ \left . \eqalign { \begin{align*} y_1' & = 0.01 - (0.01+y_1+y_2)(1001+y_1)(y_2+1) \\ y_2' & = 0.01 - (0.01+y_1+y_2)(1+y_2^2) \\ y_1(0) & =0 \\ y_2(0) & =0 \\ \end{align*} } \right . \tag{A.6} \] なお、解析解はない。

ODEPACK、VODEのAdams法では解けない。Semi-implicit RK(2step)、Recipe 77のBulirsch-Stoer法では初期値付近の解の精度が悪い。そのほかの方法では解けている。

先頭に戻る

例題４¹¹⁾：連立微分方程式の解法

同様に図書¹¹⁾にあるサンプルで、連立微分方程式の右辺が非線形となる例題である。

例題４：スティッフな微分方程式の解

次の連立微分方程式をスティッフな解法を用いて、ステップ幅0.1とし、ステップ数100まで解きなさい。なお初期刻み幅を1.E-5とする。 \[ \left . \eqalign { \begin{align*} y' & =100(\sin x -y ) \\ y(0) & = 0 \\ \end{align*} } \right . \tag{A.7} \] なお、解析解は次のとおり。 \[ \begin{align*} y & = \frac{\sin t -0.01 \cos t + 0.01 \exp( -100t)}{1.0001} \tag{A.8} \end{align*} \]

Recipe 77のRosenbrook法、Bulirsch-Stoer法では初期値付近の解の精度が悪い。そのほかの方法では解けている。

先頭に戻る

例題５⁷⁾：連立微分方程式の解法

図書⁷⁾にあるサンプルで、連立微分方程式の右辺が非線形となる例題である。

例題５：スティッフな微分方程式の解

次の連立微分方程式をスティッフな解法を用いて、ステップ幅0.5とし、ステップ数100まで解きなさい。なお初期刻み幅を1.E-5とする。 \[ \left . \eqalign { \begin{align*} y_1' & =-0.013y_1 -1000 y_1y_3 \\ y_2' & =-2500 y_2y_3 \\ y_3' & =-0.013y_1 -1000 y_1y_3 -2500y_2y_3 \\ y_1(0) & =1 \\ y_2(0) & =1 \\ y_3(0) & =0 \\ \end{align*} } \right . \tag{A.9} \] なお、解析解は得られていない。

ODEPACK、VODEのAdams法では解けない。Semi-implicit RKでは初期値付近の解の精度が悪い。そのほかの方法では解けている。

以上の例題１から例題５を、それぞれ14種類のコードで解いたが、すべての問題で正常に、しかも安定して解を与えたのは次の方法であることがわかった。

Stiffな微分方程式の安定解法
1) Gear（Private）
9) Gear（odepack）
10) LSODE（odepack、Auto BDF）
14) BDF（VODE pack）

Gear法でも問題やコードにより解ける場合と解けない場合があり、解いて見なければわからないことがあるが、ODEPACKのBDF法は最新版だけあって大抵の場合解けるようである。

先頭に戻る

化学工学への応用

Stiffな連立微分方程式を解く、極めて簡単な例を示す。工学分野、特に化学工学分野では反応器内の反応シミュレーションに、Stiffな連立微分方程式が現れる。

特に、気相の素反応を考慮した反応系では、例えばラジカル種が30個あるとき、30元の連立微分方程式を安定して解かなければならない。素反応の中には速い反応や遅い反応が混在しており、安定な解法が必要となる。

メタンの酸化カップリング反応の例^L1406)（注）では、164個の素反応、30個のラジカルの一次元プラグフロー反応器のシミュレーションを実行している。プラグフロー反応器では距離を独立変数とするが、滞留時間を独立変数とすれば非定常のバッチ反応器と同等であり、 30個の濃度の時間変化を、与えられた素反応の反応速度式を用いて解いている。

（注）：メタンと酸素を気相で酸化反応させることにより、C2以上の炭化水素を得ようとする反応。

素反応の反応速度定数は、(7)式で表され、164個の素反応の定数 A,b,Eが与えられている。 \[ \begin{align*} k & = A T^b \exp \big( - \frac{E}{RT} \big) \tag{7} \end{align*} \]

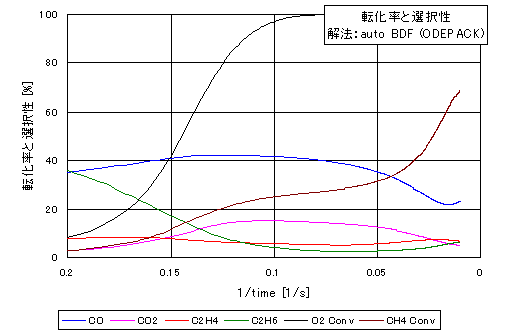
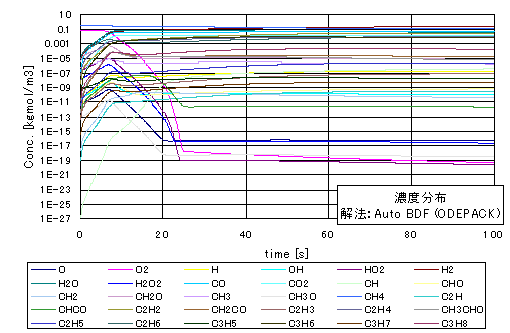
この場合、連立微分方程式はStiffとみなされ、上に述べた方法を使わないと解くことができない。 ODEPACKのBDF法を用いて計算した結果のうち、転化率と選択率の時間変化、それぞれのラジカルの時間変化の計算値を図１および図２に掲載する。

図１：転化率と選択率の変化、BDF(ODEPACK)による解

図２：ラジカル濃度の変化、BDF(ODEPACK)による解

Gear法(Private, ODEPACK)およびVODEのBDF法でもほぼ同様な結果が得られている。 IMSL法のGear法は途中エラーでストップする。

図２に示すように濃度範囲は1E-27から1.0付近までと、極めて広い濃度範囲をとる。

先頭に戻る

例題ほかの解答

上の例題の解答、および関連ファイルのダウンロードは、こちら（未リンク）で取り扱っています。

先頭に戻る

Literature Cited

引用文献
1) 化学工学会編：「改訂６版、化学工学便覧」、丸善(1999).
2) 日本機械学会編：「流れの数値シミュレーション」、コロナ社(1989).
3) 森口、宇田川、一松：「数学公式 I,II,III」、岩波(1973).
4) Fletcher,C.A.J:”Computational Techniques for Fluid Dynamics, Vol.1&2”,2nd Ed. Springer-Verlag(1991).
5) 城塚、平田、村上：「化学技術者のための移動速度論」、オーム社(1973).
6) 渡部、名取、小国：「数値解析とFORTRAN」、第３版、丸善(1983).
7) Press,W.H.,S.A.Teukolsky,W.T.Vetterling and B.P.Flannery:"Numerical Recipes in Fortran 77",2nd Ed., Cambridge (1992).
8) Press,W.H.,S.A.Teukolsky,W.T.Vetterling and B.P.Flannery:"Numerical Recipes",3rd Ed., Cambridge (2007).
9) 山田：「化学工学のための数値計算法」、槇書店(1982).
10) 杉江ら：「FORTRAN77による数値計算法」、培風館(1986).
11) 大野、磯田監修：「新版数値計算ハンドブック」P.199、オーム社(1990)
12) Gear,C.W.:"Numerical Initial Value Problems in Ordinary Differential Equations", Prentice-Hall Inc.(1971).
L1406) Geerts,J.W.M.H.,O.Chen,J.M.N.van Kasteren and K.van der Wiele:Catal.Today,6, 519-526(1990).

先頭に戻る