数値解析：線形方程式の解法（その２）

現在工事中です。ここでは連立一次方程式の係数行列が正方行列となる場合の解法の計算速度を、前報に引き続き実施した。

前報のルーチン以外の、新たなコードが公開されている解法を取り上げた。

1. 追加された連立一次方程式の解法
2. 解法の概要（追加分）
3. 解法の計算速度比較
4. 解法のまとめ
5. Literature Cited

【注】数式表示にはMathJaxを利用しています。IE8以下では表示が遅くなる可能性があります。FireFox などIE8以外のブラウザを利用下さい。

追加された連立一次方程式の解法

\[ \begin{align*} \end{align*} \]

以前、報告した連立一次方程式の解法以外に、図書・インターネットなどに公開されているソースコードを取り上げ、同様な計算速度の比較を行った。ここで取り上げたルーチンはいずれも、1990年代のベクトル型スーパーコンピュータを対象に開発されたコードであり、現在のマルチコアベースのCPUベースに開発されている訳ではない。

したがって、マルチコア用にチューニング・改良することによりさらに高速化することができる可能性が高い。

OpenMPといった並列化規格を採用した、高速化もあるが、ここでは取り上げず、別途取り上げるつもりである。

なお計算速度計測のためのコンパイラは、Intel社の Intel Visual Fortran (Intel Composer XE 2013)を用いコンパイル・リンクしている。またコンパイラ・オプションとして、"/O3"（速度優先最適化）、"/parallel"（自動並列化）を採用した。

先頭に戻る

解法の概要（追加分）

ここで追加された解法を表１に示す。主に小国らの図書¹⁰⁾、大野らの図書⁸⁾、"Numerical Recipe"⁹⁾が主なものである。

表１：正方行列を係数行列とする連立一次方程式の解法
コード名	出典	概要
mkl-LIB	6)	部分ピボット選択を利用するLU分解法
GLU1	10)	ガウス消去法
GLU2	10)	ガウス消去法（二段同時）
GLU4	10)	ガウス消去法（二段二列同時）
GLUB1	10)	縦ブロックガウス法
GLUB2	10)	縦ブロックガウス法（二段同時）
GLUB4	10)	縦ブロックガウス法（二段二列同時）
SLU1	10)	対称ガウス法、N>30のとき誤差大きい
SLU2	10)	対称ガウス法（二段同時）、N>30のとき誤差大きい
SLU4	10)	対称ガウス法（二段二列同時）、N>30のとき誤差大きい
BLPIVT	8)	ブロック対角ピボッティング法、コード異常
CHLSKY	8)	LU分解、コード異常
COMPCT	8)	LU分解、他の解法に比べ遅い
LNQGJ	8)	ガウスジョルダン法、他の解法に比べ桁違いに遅い
DLINLD	3)	改訂コレスキー、N>30のとき誤差大きい
GAUSSJ	9)	ガウスジョルダン法、他の解法に比べ桁違いに遅い
LUDCMP	9)	LU分解、他の解法に比べ遅い
CHOLDC	9)	コレスキー分解、コード異常
QRDCMP	9)	QR分解
SVDCMP	9)	SVD分解、N大きいとき結果異常

先頭の"mkl-LIB"は、Intel MKLライブラリにある解法を示す。これは前報の結果との比較のため入れてある。

なお概要欄にはデバッグ時に得られた情報もまとめている。これら情報は使用方法を単純に間違えているものもあるかも知れぬが、小スケール（Nが10以下）のテスト例によるデバッグを経ており、”コード異常”を除き、その段階で正解が得られている。

先頭に戻る

解法の計算速度比較

取り上げた例題を、例題１に示す。これは前報と全く同じ例題を採用し、比較のベースが同一となるように設定した。

例題１：連立一次方程式のサンプル

n元の係数行列\( {\bf A} \)の要素\( a_{i,j} \)を次式で与える。 \[ \begin{align*} a_{i,j}=\sqrt{ \frac 2 {n+1}} \sin( \frac {\pi ij}{n+1}) \tag{3} \end{align*} \] そして、解ベクトル \( \bf x \) の要素\( x_i \) を次のように \[ \begin{align*} x_i= i \tag{4} \end{align*} \] 与え、右辺ベクトル \( \bf b \) を、係数行列と解ベクトルから算出し、セットする。

表１に示す新たに追加したルーチンと、前報で用いたルーチン（一部取捨選択している）とを比較のため同時に計測した。コンパイルは32bitアプリとしてコンパイルし、Windows 7(64BitOS）上のDos Promptから起動している。前報と日を違えているため実行時の環境（バックグラウンド・ジョブの有無など）が違い計測誤差、バラツキがあることに注意されたい。

計測結果を表２に示す。またコンパイル・リンク時のオプションとライブラリ指定（MKLライブ）をリスト１に示す。

リスト１：コンパイル・リンクオプション

#コンパイルオプション
FOR_OPT=/O3 /Qparallel /Qpar-report1 /Zi	# 自動並列化

##### static link, parallel version, cdecl
LIBMKL=	mkl_intel_c.lib  mkl_intel_thread.lib \
	mkl_core.lib   libiomp5md.lib

表２の中で、10番目から16番目が今回追加した、安定した解法の計算時間である。この中でGLU4のみが前報で紹介した高速解法に比肩する性能を示しており、これ以外はそれほど性能の良い解法とは言えない。

表２：連立一次方程式の解法：計算時間の計測（ミリ秒）
	N	1000	2000	4000	5000
1	LU22	410	2430	22970	44510
2	SAXGLU	430	3930	33070	63840
3	USAXGL	410	3510	27630	53530
4	WSAXGL	340	2280	17420	34130
5	BGAUSS	400	3730	32050	62770
6	USHIJM	450	4930	40360	79990
7	mkl-LIB	60	490	2260	4010
8	LAPACK	410	4910	40010	79290
9	M_LEQ	1070	11520	93650	184510
10	GLU1	460	4930	40310	80030
11	GLU2	300	3090	24490	48400
12	GLU4	290	2820	22070	43030
13	GLUB1	420	4170	37000	74820
14	GLUB2	450	4460	37550	74070
15	GLUB4	400	3940	33190	65700
16	QRDCMP	600	6550	60420	121140

得られた結果を図１にプロットしている。計算時間を縦軸に、横軸に正方行列の次元数を片対数でプロットした。図からやはりIntel のMKL ライブラリが圧倒的に、桁違いに速いことが分かる。

新たに追加したルーチンのうち、GLU4が割合に速いことが分かるが、前法との比較でいうとWSAXGLが自動並列化、速度優先最適化のコンパイルでは最も速い。

OpenMPを利用した並列化の効果は現在のところ試していないので不明だが、MKLライブラリに近い性能をたたき出せる可能性はあると思う。

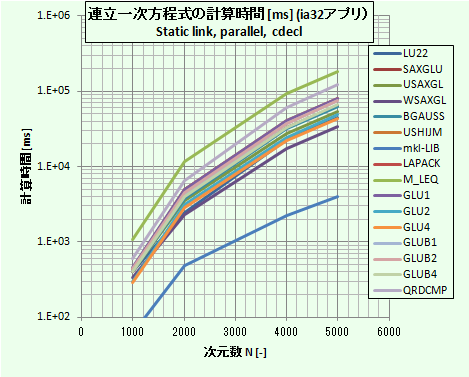
図１：解法の計算時間比較

先頭に戻る

解法のまとめ

正方行列を係数行列とする連立一次方程式の解法で、大規模なもの（N>1000）はIntel社のMKLライブラリにあるルーチンが、マルチコアに対応した並列化コードであり、試験したコードの中で圧倒的な速さを示している。

ソースコードが開示されていないという使用上の不便さはあるものの、解を安定して得られるコードであるなら置換して利用することにより速度面でのメリットが活かせると思われる。ソースコードのある別の解法を開発当初は利用し、バグがほとんど出なくなってからMKLライブに置き換えるという方法が良さそう。それも大規模になればなるほど速度面でのメリットは大きい。

ここで示したサンプルファイルおよび関連ファイルのダウンロードは、ここ（未リンク）で取り扱っています。

先頭に戻る

Literature Cited

FORTRANなどの言語を用いた連立一次方程式の解法のソースコードが記載されている図書・パッケージを以下に掲げる。

4),6)を除き、多くの図書は1990年代のスパコン全盛期に刊行されたもので、当時のベクトル計算機向けに開発されたコードが多い。

引用文献・参考図書
1) 島崎著：「スーパーコンピュータとプログラミング」、共立出版(1989).
2) 村田、小国、唐木著：「スーパーコンピュータ」、丸善(1986).
3) 渡部、名取、小国著：「数値解析とFORTRAN」第３版、丸善(1983).
4) 牛島著：「OpenMPによる並列プログラミングと数値計算法」、丸善(2006).
5) 戸川隼人著：「新装版科学技術計算ハンドブック基礎篇C言語版」、サイエンス社(2002).
6) インテル：マス・カーネル・ライブラリー（Intel MKL).
7) LAPACK：Linear Algebra PACKage, Netlib(www.netlib.org).
8) 大野、磯田監修：「新版数値計算ハンドブック」P.16、オーム社(1990)
9) Press,W.H.,S.A.Teukolsky,W.T.Vetterling,B.P.Flannery:"Numerical Recipes in FORTRAN 77",2nd Ed.,Cambridge Univ.Press.(2001).
10) 小国力編著：「行列計算ソフトウェア、WS,スーパーコン、並列計算機」、丸善(1991).

先頭に戻る