トップ > ライブラリ > 数値解析 > 非線型方程式

数値解析：非線型方程式

現在工事中です。 取り敢えず繋がりましたが、まだまだ未完成（これからも更新する予定）です。

【注】数式表示にはMathJaxを利用しています。IE8以下では表示が遅くなる可能性があります。FireFox などIE8以外のブラウザを利用下さい。

先頭に戻る

非線型方程式とは

ここでは線形代数方程式(linear algebraic equations)ではなく、非線型の（連立）代数方程式の解法について 述べる。線形の代数方程式については、こちら数学・算術演算を参照されたい。

非線型の代数方程式で、一変数の方程式となると非整数次の高次多項式などに相当するが、一変数の非線型代数方程式および 多変数の連立非線型代数方程式の解法は、特別な場合を除き、代数演算で解くことはできず収束計算となる。

一変数の二次多項式については解析的に解が求められており、 \[ \begin{align*} ax^2+bx+c =0 \tag{1} \\ x = \frac {-b \pm \sqrt{b^2-4ac}}{2a} \tag{2} \\ \end{align*} \]

で与えられる。また一変数の三次多項式も解析的に、Cardano法と呼ばれる方法で解を求めることができる。 4次以上の多項式になるともはや解析的に解くことができず、以下に述べるNewton法などによる収束計算で 解を求め、順次、減次して行く方法となる。

一方、多変数の非線型方程式は、ひとつの変数が高次項で現れたり、複数の変数が乗除算や他の数学関数で で現れたり、枚挙に暇ない。多変数の非線型方程式を、以後、連立非線型方程式というが、主にこの方程式の解法について述べる。単に非線型方程式と呼ぶときは連立非線型方程式を指すものとする。

先頭に戻る

化学工学における非線型方程式

化学工学の分野では、熱力学や物理化学などを基礎とし、単位操作や反応操作などで組み立てられているが、基本的に物質収支式や熱収支式を基礎におく限り、すべてが非線型方程式を構成している。

ある単純な仮定を置くことにより線形方程式に変換し、解析解を得やすくし、モデルの簡略化を行う。たとえば理想気体のラウールの法則、理想溶液の活量係数を１とするなどが上げられる。化学工学に限らず、あらゆる 自然現象はもともと非線型でありそうなことがわかる。

反応を伴う現象を表す、常微分方程式や偏微分方程式なども、差分化することにより、非線型方程式に変換することができる。反応項はもちろん等温の一次反応であれば線形であるが、非等温であれば速度定数に温度依存項が 現れ、非線型となる。またPVT物性や輸送物性のような現象をあらわす基礎方程式に現れる物性値は、純成分は別にして温度、組成に依存するため、非線型となる。

先頭に戻る

非線型方程式の解法

一変数の高次代数方程式で、2次および3次までの代数方程式は上に述べたように解析解が求められている。 3次の代数方程式の代表的なものとして、Van der Waals型の状態方程式がある。Peng-Robinson（PR）、Redlich-Kwong（RK)、Soave-RK（SRK）など有名な 状態方程式はモル容積を変数とする3次方程式であり、Cardano法で解析的に解くことができる。

4次以上になると、解析解は得られておらず、収束手法を用いた計算法を適用しなければならない。4次以上のときには根を収束手法により、ひとつ求めると、元の代数方程式の次数が減る（減次）ことを繰り返し、すべての根を求める（複素根を含めて）。 高次代数方程式の解法でひとつの根を求める方法には、

などが有名であり、一変数のときの求根には適した方法といえる。

一方、多変数の連立非線形方程式系では、

など、Newton法をオリジナルとする一階微分（勾配）を利用する方法が多数を占めている。オリジナルなNewton法はそのアルゴリズムが簡便であること、初期値を適当に与えることにより２次関数的な収束性を示すこと、収束安定性が高いことなどメリットは多く、工学系の非線形問題の解法として多く利用される。Broyden法、Powell法、CGMなどどちらかというと数学的に非線形性の高い問題に対処したもので、工学的な利用価値は低い（私見ではあるがそれほど特殊な非線形性はめったに遭遇しない）。

また、Broyden法以下の方法は取扱がアルゴリズムが複雑であり、理解するのに難点がある。化学工学計算で現れる非線形性は、大概オリジナルのNewton法で、安定的に解くことが可能である。

非線型連立方程式を解くとき、勾配を用いるニュートン法（タイプＡとする）以外に、次のように発想を変換したタイプが存在する。

タイプＢは、本来の目的関数 \( f(x)=0 \) となるところを、\( f^2(x) \to {\rm min.} \) と目的関数の2乗をとり非負の新たな目的関数を最小化する最適化問題に変換して解く方法である。これら既存のコード、出典など詳細をAppendix-A：連立非線型方程式の解法一覧（未リンク）に示す。

またタイプＣとも関連して、非線形連立微分方程式でStiffな系を解く方法の一覧をAppendix-B：非線型連立微分方程式の解法（未リンク）に示す。

タイプＤは、Newton法に類似しているが、水中のイオン濃度のように101から10-14のような濃度範囲が極めて広いとき、しかも負組成を取らない場合に、これら濃度の対数に変数変換して解く、特殊な解法である。

先頭に戻る

Newton法による解法

ここでは非線形方程式を解くためのニュートン法（Newton-Raphson法ともいう）について基礎を習得する。

Newton法の基礎

一変数の関数 \( f(x) \) を考え、\( x_1 \) まわりでのTaylor展開を考えると、\( f(x) \) は次のように近似できる。 \[ \begin{align*} f(x) = & f(x_1)+f'(x_1)(x-x_1)+\frac{1}{2!}f''(x_1)(x-x_1)^2 + \cdots \\ & +\frac{1}{n!}f^{(n)}(x_1)(x-x_1)^n+ \cdots \tag{3} \end{align*} \]

Taylor展開した関数 \( f(x) \) の一階微分項までをとり、また、\( \Delta x=x-x_1 \) と定義すると、(3)式は、 \[ \begin{align*} f(x_1+\Delta x) = & f(x_1)+f'(x_1)\Delta x \tag{4} \end{align*} \]

と表される。この式は \( \Delta x \) に関し線形化されている。 いま、 \( f(x)=0 \) を満たす独立変数 \( x \) を求めることを考え、初期値 \( x_1 \) での関数の値 \( f(x_1) \) と一階の微係数の値 \( f'(x_1) \) が求められると、(4)式から、 \( f(x_1+\Delta x)=0 \) を満たす修正幅 \( \Delta x \) が次のように求められる。そして、次の新しい初期値 \( x^{(n+1)} \) が求められる。 \[ \begin{align*} \Delta x & = -\frac{f(x_1)}{f'(x_1)} \tag{5} \\ x^{(n+1)} & = x_1+\Delta x \tag{6} \end{align*} \]

この操作を繰り返しもとめ、最終的にゼロにきわめて近いεを判定条件とし、関数の値が次式を満足するまで独立変数を収束させる。 \[ \begin{align*} \bigl| \ f(x) \ \bigr| < \varepsilon \tag{7} \end{align*} \]

図１：Newton法の初期値

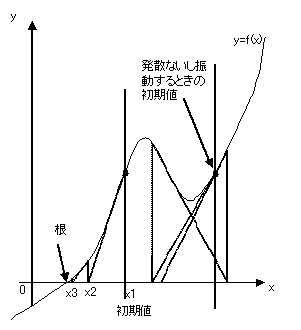
図１に示すように、 \( f(x)=0 \) を満足する根を探索するとき、与える初期値により、解が収束したり、発散・振動したりする。偏曲点をまたぐときや、関数形状が異常なとき以外で、局所的に二次関数的であれば、Newton法は安定的に、また急速な収束性を示す。

Newton法では関数 \( f(x) \) の一階の微係数 \( f'(x) \) を計算する必要があるが、関数形がきわめて簡単で微分式が容易に求められるとき以外は、数値微分を用いたコーディングを行う。特に反応工学の問題では目的関数 \( f(x) \) が複雑な場合が多く、解析的な微分式を現実問題として得ることができず、数値微分を利用することが多い。リスト１に一変数のNewton法のVBAコードの例を掲載する。

リスト中の関数"problem_01_obj( x,b )"は関数 \( f(x) \)を返し、引数 bは関数の中で使う変数を示す。

リスト１：１変数Newton法のサンプル（VBA） 

  X# = 0.5           		' 初期値をセット
  For it = 1 To ITMAX		' 収束ループ、Newton法ではITMAX=20程度でほとんど収束
'
    OBJ# = problem_01_obj(X#, A)	' 独立変数X#で、関数値f(x)を計算し、OBJ#に代入
    If Abs(OBJ#) <= EPS Then GoTo exit_loop   ' OBJ#の絶対値がEPS以下のとき、exit_loopにジャンプ
    x1# = X# * (1# + DX)		' 初期値からX#*DXだけ増加させる
    obj1# = problem_01_obj(x1#, A)	' x1#での目的関数値を計算。独立変数以外の引数も渡す
    dobj# = (obj1# - OBJ#) / (X# * DX)	' 一階の微係数を計算（数値微分を利用）
    xold# = X#			' X#を一時保存
    X# = X# - OBJ# / dobj#		' 新しいX#を計算
    If X# < 0# Then X# = 0.5 * xold#		' X#が負になったときの処置
    If X# > 1# Then X# = 0.5 * (1# + xold#)	' X#が１以上のときの処置
  Next it
'						’ITMAXを越えた時
  MsgBox "収束しませんでした", , "演習１"
exit_loop:					’収束条件を満足したときのジャンプ先ラベル
  problem_01 = X#

収束判定条件εの与え方は、1.E-7（正規化して）程度。微係数を求めるときの増分として、リスト１の変数DXとして 1.E-5程度（場合にもよるが、微係数をある程度の精度で評価できる値を採用すること）をとる。後述するよう収束判定基準は、熱収支や物質収支の単位系に大きく依存し、これらを横並びに評価・判定するときそれぞれの保存則を正規化して、評価する必要がある。

先頭に戻る

多変数のNewton法

本ウェブサイトの別のところでも述べたように、反応を含む保存則を差分化すると、非線形連立方程式系に帰着することを解説した。ここでは、多変数の非線型連立方程式の解法にNewton法を適用する。

n個の独立変数 \( x_1,x_2,\cdots,x_n \) （n次元空間）をもつ、n個の目的関数 \( f_i(x_1,x_2,\cdots,x_n)=0, (i=1,n) \) について考える。目的関数は任意の関数であり、独立変数に対して非線形であるとする（代数的に解けない）。この目的関数を満足する解を求めることを考える。

一変数のときと同じく、n次元空間中の１つの点 \( x_1^0,x_2^0,\cdots,x_n^0 \) で、Taylor展開をとる。 \[ \begin{align*} f_i( x_1,x_2,\cdots,x_n ) & =f_i( x_1^0,x_2^0,\cdots,x_n^0)+\sum_{j=1}^n \frac{\partial f_i}{\partial x_j} \biggr| _{x=x^0}(x_j-x_j^0) \\ & +\cdots, (i=1,n) \tag{8} \end{align*} \]

右辺第2項の総和は、各座標方向の微係数を係数とする線形結合をしていることがわかる。 目的関数がゼロ（左辺がすべてゼロ）となるよう、修正幅 \((x_j-x_j^0)\) を求める線形の連立方程式に変換されていることがわかる。 連立方程式を解くために、右辺の第1項および第2項の微係数の値を、 \( x_1^0,x_2^0,\cdots,x_n^0 \) で評価し、求める必要がある。 (8)式の左辺がゼロとなる修正幅 \( \Delta x \) を求めるには、次の(9)式の線形連立方程式を解けばよい。 右辺第１項は、初期点での目的関数値であり、第２項の係数行列は目的関数の一階微係数行列（ \( \displaystyle {\bf{J}=\frac{\partial \bf{F}}{\partial \bf{x}} } \) 、これをヤコビ行列、Jacobian Matrixという）であり、初期点での目的関数を偏微分することにより求められる。 行列・ベクトル表示（太文字表示）すると、(10)式のように表記される。(10)式左辺はゼロベクトルである。(11)はJacobian Matrixの定義である。

【注】ヤコビ行列の縦横の添字に注意されたい。第(n,m)要素は、n番目の目的関数を、m番目の独立変数で偏微分したものが入る。 \[ \begin{align*} \left[ \begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \\ \end{array} \right] = \left[ \begin{array}{c} f_1 \\ f_2 \\ \vdots \\ f_n \\ \end{array} \right] + \left[\begin{array}{cccc} \frac {\partial f_1}{\partial x_1} & \frac {\partial f_1}{\partial x_2} & \cdots & \frac {\partial f_1}{\partial x_n} \\ \frac {\partial f_2}{\partial x_1} & \frac {\partial f_2}{\partial x_2} & \cdots & \frac {\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac {\partial f_n}{\partial x_1} & \frac {\partial f_n}{\partial x_2} & \cdots & \frac {\partial f_n}{\partial x_n} \end{array}\right] \left[ \begin{array}{c} \Delta x_1 \\ \Delta x_2 \\ \vdots \\ \Delta x_n \\ \end{array} \right] \tag{9} \end{align*} \] \[ \begin{align*} {\bf 0} & ={\bf F}({\bf x})+\frac{\partial {\bf F}}{\partial {\bf x}} \Delta {\bf x} \tag{10} \\ {\bf J} & =\frac{\partial {\bf F}}{\partial {\bf x}} \tag{11} \end{align*} \]

線形の連立方程式(9)または(10)式を解き \( \Delta \boldsymbol{x} \) を求めると、次のように表され、複数の独立変数をもつNewton法は、これを繰り返すことにより、解を得る。(12)式の表記でべき乗(-1)は、逆行列を意味している。 \[ \left. \eqalign { \begin{align*} \Delta {\bf x} & =-{\bf J}^{-1} {\bf F}({\bf x}) \\ {\bf x}^{n+1} & ={\bf x}^n-{\bf J}^{-1} {\bf F}({\bf x}^n) \\ \end{align*} }\right. \tag{12} \]

【注】ヤコビ行列は、\( {\bf x}^n \) での一階微分値であり、毎回更新されるべきであるが、解に近づくにつれ、ヤコビ行列の変動は少なくなる。従って、毎回ヤコビ行列を計算せず、前回のヤコビ行列を流用する方法も大規模な連立方程式を解くときには行われる。

先頭に戻る

連立の離散化方程式とヤコビ行列

本サイトの反応器シミュレーションで、反応を含む保存則を離散化した差分方程式は非線形連立方程式を構成していることを示した。

いまメッシュ点ｊの差分化方程式で、独立変数の部分ベクトル \( {\bf x}_j \) 、および目的関数を表す部分ベクトル \( {\bf y}_j \) を次のように定義している。 \[ \left. \eqalign { \begin{align*} {\bf x}_j & =[C_{1,j},C_{2,j},\cdots,C_{M,j},u_j,T_j,P_j]^T \cr {\bf y}_j & =[M_{1,j},M_{2,j},\cdots,M_{M,j},O_j,E_j,B_j]^T = {\bf 0} \cr \end{align*} }\right\} \tag{13} \]

ここで、上付添字\( \it T \ \)は、転置ベクトルを示す。さらに、メッシュ点の数を \( N \) 個とし、 上の部分ベクトルを要素とする解析領域全体（反応器全体）の目的関数ベクトル \( {\bf y}= {\bf F}({\bf x}) \) および独立変数ベクトル \( {\bf x} \) を次のように定義し、解析領域全体の支配方程式を表した。 \[ \left. \eqalign { \begin{align*} {\bf x} & = [ {\bf x}_0,{\bf x}_1,\cdots,{\bf x}_N]^T \cr {\bf y} & = [ {\bf y}_0,{\bf y}_1,\cdots,{\bf y}_N]^T ={\bf 0} \cr \end{align*} }\right\} \tag{14} \]

従って、次のベクトル式を満足する、独立変数 \( {\bf x} \) を求める問題に帰着する。 \[ {\bf y}={\bf 0} \tag{15} \]

右辺 \( {\bf 0} \) は、ゼロベクトルを示す。目的関数ベクトルおよび独立変数ベクトルの要素の数は、成分数がMの場合は、(M+3)*(N+1)個となる。差分化した保存則は(15)式で表される非線形連立方程式となる。 いま（15）式を解くため、前節の多変数のNewton法を適用し、\( {\bf x} = {\bf x}_1 \) の廻りTaylor展開し、１次微分項までとると、 \[ \begin{align*} {\bf F}({\bf x}_1+\Delta {\bf x})={\bf F}({\bf x}_1)+\Delta {\bf x} \frac{\partial {\bf F}}{\partial {\bf x}} \biggr|_{{\bf x}={\bf x}_1} \tag{16} \end{align*} \]

となる。右辺の第2項の微係数項（ヤコブ行列）は（M+3)*(N+1)の正方行列となる。これを \( \Delta {\bf x} \) について変形し、左辺の目的関数がゼロとなるよう修正幅 \( \Delta {\bf x} \) を決めるには、(16)式をゼロとおき、 \( \Delta {\bf x} \) についての線型連立方程式を解けばよい。 \[ \Delta {\bf x}=- \biggl[\frac{\partial {\bf F}}{\partial {\bf x}}\biggr]^{-1}{\bf F}({\bf x}_1) \tag{17} \]

得られた修正幅 \( \Delta {\bf x} \) に緩和係数ωを導入し、目的関数値がゼロと考えられる次の独立変数ベクトル \( {\bf x}_2 \)が次式により算出できる（注１）。 \[ {\bf x}_2={\bf x}_1+\omega\Delta {\bf x} \tag{18} \]

目的関数がすべての独立変数に対して線形であれば、\( {\bf x}_2 \) ベクトルは目的関数をゼロにするが、 非線形の場合には通常ゼロにはならず、 \( {\bf x}_2 \)を \( {\bf x}_1 \)に置き直し、(17)式および（18）式を繰り返し解くことになる。

【注１】緩和係数ωは、通常ω=1を採用するが、初期値が全く不明で、解が振動しやすい場合に、その変動幅を抑制するために、ω=0.5～1.0の値が使われることがある。特に反応温度など温度の少しの変動で反応速度が大きく変動し、解を求めることが困難な場合があり、こうした温度変動をある程度抑制する必要があるとき緩和係数を利用することがある（次節参照）。

ここで、ヤコビ行列の要素について以下考察する。分割数N、成分数Mのとき、ヤコビ行列は、数学的には(M+3)*(N+1)個の要素を一辺とする正方行列になっている。

しかし、例えば第ｊ番目のメッシュ点での保存則を考えると、反応器シミュレーションのページの図（未リンク）で示したように、j-1点、ｊ点、およびj+1点の値だけから目的関数部分ベクトルは計算できる。これ以外の点からの寄与はない。

目的関数を独立変数で偏微分して得られるヤコビ行列を考えると、0からj-2点、およびj+2点からN点までの部分行列（別ページの図の部分行列 \( {\bf A}_j,{\bf B}_j,{\bf C}_j \) 以外のところ）は、すべて要素がゼロの行列となっている。というのは目的関数は、これらメッシュ点に無関係であり、式の中に入っていない。

従って、保存則を差分化したとき、ヤコビ行列は少なくとも3*(M+3)の幅をもつバンド行列（Band Matrix)となっている。バンド行列であれば正方行列に比べ配列サイズが小さく、逆に言えばより大きな問題が解けることになる。

さらにヤコビ行列の部分行列 \( {\bf A}_j,{\bf B}_j,{\bf C}_j \) の詳細を見る。

部分行列 \( {\bf A}_j \) は、第ｊ番目の目的関数部分ベクトルのj-1番目の変数ベクトルによる偏微分である。

同様に、部分行列 \( {\bf C}_j \) は、第ｊ番目の目的関数部分ベクトルのj+1番目の変数ベクトルによる偏微分である。

目的関数部分ベクトルの個々の要素を見ると、非線形項は反応項だけであり、反応項は第ｊ番目の変数ベクトルだけに依存するため、部分行列 \( {\bf A}_j,{\bf C}_j \)の２つは、対角だけに要素がある部分行列となっている。

部分行列 \( {\bf B}_j \)は、第ｊ番目の目的関数部分ベクトルのj番目の変数ベクトルによる偏微分であり、反応項があるため、部分行列のほとんどの要素が非ゼロとなり、（M+3）×(M+3)の正方行列を構成している。

ヤコビ行列は、つぎのようなバンド行列となり、計算機リソースの節約となる。 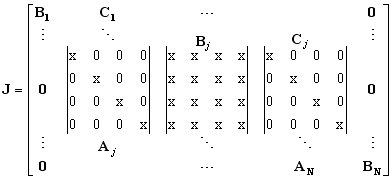\( \tag{17} \)

先頭に戻る

修正Newton法

ニュートン法を利用する場合の、収束のテクニック、コードを作成するときのテクニックを以下に述べる。「修正Newton法」ということばは世の中には認知されていない。ここだけの話。

緩和係数

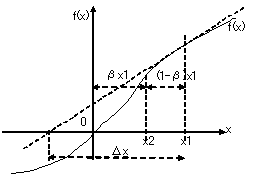
通常のNewton法では緩和係数ωとして1.0を採用するが、目的関数の形により、0.5から1.0の間の値を採用することもある。独立変数が１つのときの緩和係数の概念を、図２に示す。値1.0以上の過緩和は、通常めったに採用しない。

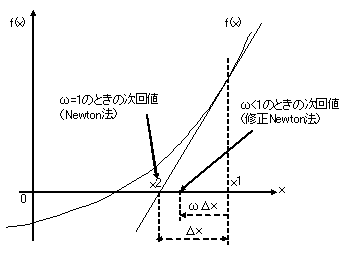
図２：Newton法の緩和係数の概念

目的関数 \( {\bf F}({\bf x}) \)がゼロに達したかどうかを判定するとき、目的関数ベクトルをまず正規化する必要がある。正規化とは、おおもとの差分方程式の目的関数値 \( M_{i,j} \) など、両辺を非ゼロの移流項の \( u_jC_{i,j} \) で除し、1.0に対してどの程度ゼロに近づいているか相対的な値を得ることをいう。熱収支、圧力収支もそれぞれの式で正規化を行なう。こうしてすべての目的関数ベクトルの要素 \( F_j,(j=1,N) \)をすべて正規化し、そのノルム \[ \bigl\|{\bf O}\bigr\| = \frac{1}{N} \sqrt{\sum_{j=1}^N F_j^2} \tag{20} \]

を使い、収束判定を行なう。ノルムは(20)式で定義されるように、ベクトルの要素 \( F_j,(j=1,N) \) の二乗和の平方根を要素数Nで割った値（統計量でいう標準偏差に相当）であり、1.0に対して相対的にどの程度ゼロに近づいているか要素ひとつ当りの平均誤差を示している。

先頭に戻る

負の物理量処理

図３：負の物理量のときの処理

Newton法により、独立変数を(18)式で修正するとき、物理量である独立変数が負になる場合がありうる。図３に示すように、目的関数の形により、次回値が負の値になることがある。独立変数として、成分のモル濃度、絶対温度、絶対圧力などの物理量を採用しており、通常負の値をとることはありえない。そこで、収束計算の続行を可能にするため、負組成の処理をする必要がある。通常の化学反応のような反応速度を含むシミュレーションでは、モル濃度のｎ次反応のようにべき乗が含まれ、負組成のまま反応速度計算をすると、負のべき乗エラーが起こり、計算を続行することはできない。

負組成などの処理方法は、スカラー量β（入力データや固定値となる）を導入し、 \[ {\bf x}_2= \beta({\bf 0}+{\bf x}_1) \tag{21} \]

のように、ゼロと現在値の加重平均値を用いる方法を採用することが多い。β=0.5では算術平均に相当する。濃度のように、10のマイナス何乗のように、極めてゼロに近く、正の値をもつことが予想される場合にはβとして0.1などを採用し、解にできるだけ速く到達するようにすることもある。 逆にモル分率や重量分率など割合を表す物理量で上限のある量でも、同じように、Newton法でこの上限を越える場合がある。このときも負組成と同様に \[ {\bf x}_2= \beta({\bf x}_{\rm upper}+{\bf x}_1) \tag{22} \]

と、上限値と現在値の加重平均をとり、これを上限を越えた時の次回値とし、計算を続行させることを行う。

先頭に戻る

修正幅の制限

図４：変動幅制限をつけたときの概念

また、目的関数の形により、振動したり発散したりすることが起こる。このとき、修正幅 \( \Delta {\bf x} \) を制限することが行なわれる。 独立変数が振動したり、値自体が飛び跳ねて発散している原因は、(18)式右辺の修正幅項（\( \omega \Delta {\bf x} \) ）の値が、\( {\bf x} \) の値に比べ相対的に大きすぎることが考えられる。 修正幅項の常識的な値は、コンピュータでは判断できず、ユーザーが適宜判断することができる工夫をすることがある。

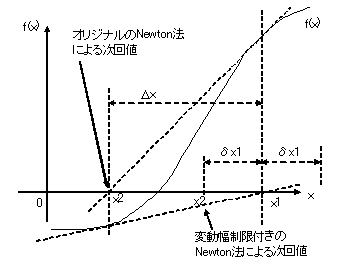
例えば、温度のように、100℃付近に解がありそうなことがユーザーには判断でき、従って修正幅として、20℃程度に制限し、 算出される \( \omega \Delta {\bf x} \) の値がこの制限値をオーバーするようであれば、制限値を採用し、温度を修正するなどすることがある。 図４に、オリジナルのNewton法（ω=１のとき）で、解が振動する例を示している。\( x_1 \) から微係数を求め、\( x_2 \) を算出し、１ステップ進んで、\( x_2 \) の微係数を求め、 目的関数がゼロとなる新しい点が、再びもとの \( x_1 \) の近くにきてしまう例である。こうした振動を防ぐため、変動幅に制限を設けることが行なわれる。

具体的には、変数の相対的な変動の大きさの制限値\( \delta \) を指定し、この \( -\delta x_1 \)から \( +\delta x_1 \) の範囲内で、変数を修正する。 \[ \begin{align*} \left. \eqalign{ \rm{when} \biggl|\frac{\omega \Delta {\bf x}}{{\bf x}_1} \biggr| \le \delta , ~~ {\bf x}_2 & ={\bf x}_1 + \omega \Delta {\bf x} \cr \rm{when} \biggl|\frac{\omega \Delta {\bf x}}{{\bf x}_1} \biggr| \ge \delta , ~~ {\bf x}_2 & ={\bf x}_1 + \rm{sign}(\Delta {\bf x}, \delta {\bf x}_1) \cr }\right\} \tag{23} \end{align*} \]

ここで、\( {\rm sign}( \Delta {\bf x}, \delta{\bf x}_1) \) は、 \( \Delta {\bf x} \) の符号を値 \( \delta {\bf x}_1 \)につける関数を意味する。

先頭に戻る

正規化と収束判定条件

成分物質収支や熱収支など基礎方程式を連立して解くとき、これら保存則が収束したかどうかは、各収支式を正規化し、それぞれの収支が収束しているかどうかを判定する必要がある。収支式では利用する単位系によりそのアンバランスの絶対値がバラバラとなっており、バラバラのままノルムを計算し、収束判定しても意味がないことになる。

正規化(Normalization、Scaling）は、たとえば、第i成分の第ｊメッシュ点の次の成分収支式において、 \[ \begin{align*} M_{i,j} \equiv & - \delta_M \frac{u_jC_{i,j}-u_{j-1}C_{i,j-1}} {z_j-z_{j-1}} - (1-\delta_M) \frac{u_{j+1}C_{i,j+1}-u_jC_{i,j}} {z_{j+1}-z_j} \\ & + \frac{2E_z}{z_{j+1}-z_{j-1}} \biggl\{ \frac{C_{i,j+1}-C_{i,j}} {z_{j+1}-z_j} - \frac{C_{i,j}-C_{i,j-1}} {z_j-z_{j-1}} \biggr\} \\ & + \rho_B \sum {\frac{w_{k,j}}{\rho_k}}r_{k,j}\alpha_{k,j} + \varepsilon_j \sum {r_{k,j}\alpha_{k,i}} = 0 \\ & (j=1,N-1,i=1,M) \tag{24} \end{align*} \]

６つの項の和で表されている（拡散項を２つと数える）。各項の絶対値の最大となる項を正規化パラメータとして採用し、両辺をこれで除し、 アンバランス \( M_{i,j} \) が絶対値1．0前後となるように正規化することを行う。

熱収支および圧力収支も各項の最大値を正規化パラメータとし、アンバランスの絶対値が1.0前後となるよう正規化を行う。そして、これら正規化された収支式アンバランスのノルムを計算し、収束判定を行う。

先頭に戻る

計算機のリソース

計算機のリソースとして、メモリ、CPUがある。

計算機のRAMメモリは、32bitOSではメモリは4GB（Windows XPでは3GB程度）が利用可能な容量となっている。Newton法取り扱う非線形連立方程式で、ヤコビ行列がメモリの大部分を占める。Fortranなどではコードはdouble精度で記述するが、Pentium IVマシンクラスでは、10000x10000の正方行列がほぼ限界と思われる。10000x10000x8で約800MBを必要とする。

先に示した第ｊ番目のメッシュ点での独立変数や目的関数の部分ベクトルを並べ、全体を構成するとき、ヤコビ行列がバンドマトリックスとなり、行列の全要素数を減らすことが可能となる。全点の独立変数の並べ方により、行列のサイズが大きく影響を受けている。

計算機のCPUについては、最近のマルチコア対応の数値計算ライブラリ、例えばIntel FortranのMKL(math kernel library)では、コードの並列化（マルチスレッドによる並列化、マルチコアによる並列化）が行われ、高速化が図られている。こうしたコードをユーザーが利用できる環境にあり、Quad CPUマシンも身近な存在となっており、ひと頃よりは高速な計算機環境にあるといえる。

先頭に戻る

演習問題

事前配布のExcelファイル02_problem.xlsのVBA（すでに大まかなルーチンは作成済み）を利用して、回答を完成・作成しなさい。

練習問題１：１変数のNewton法による収束計算

気泡塔の不均一気泡流動域のガスホールドアップの相関式に、次のAkita and Yoshidaの式[L1742] がある。純液で非電解質のとき。 \[ \begin{align*} \frac{\varepsilon_G}{(1-\varepsilon_G)^4}=0.2 \biggl( \frac{gD_T^2\rho_L}{\sigma} \biggr)^{1/8} \biggl( \frac{gD_T^3\rho_L^2}{\mu_L^2} \biggr)^{1/12} \biggl( \frac{u_G}{\sqrt{gD_T}} \biggr) \tag{25} \end{align*} \]

塔径 \( D_T \) =1.4m、液密度 \( \rho_L \)=838kg/m3、液粘度 \( \mu_L \)=0.1079cP、表面張力 \( \sigma \) =34.68dyn/cm、ガス線速度 =0.034m/sのとき、ガスホールドアップ（注１）を求めよ。ただし、塔径0.6m以上のときは \( D_T \) =0.6mを使う。

【注１】ガスホールドアップとは、反応器単位体積当たりに占めるガスの容積割合[m3-gas/m3-reactor volume]をいう。従って、ガスホールドアップは0以上1以下の有限の値をとる。
(1) XLSファイル上で手計算による収束をさせなさい（回答１）
(2) １変数の収束計算Newton法を使って、VBAコードを記述し、空隙率を求めなさい。
このとき、勾配（一階微分）は数値微分を使うこと。また、Newton法でガスホールドアップが[0,1]の範囲内になるよう、変動範囲の制約を考慮にいれなさい。

練習問題２：２変数のNewton法による収束計算

気液二相下降並流の充填層（トリクルベッド反応器）の圧力損失 \( \Delta P/L \) および液ホールドアップ \( \varepsilon_L \)を、Wammesら[L4638]の方法（概略は以下）で求めなさい。 \[ \beta_{dyn} =3.8 \biggl( \frac{\rho_L u_L d_p}{\mu_L} \biggr)^{0.55} \biggl[ \frac{d_p^3 \rho_L^2 g}{\mu_L^2} \biggl(1+\frac{\Delta P}{\rho_LgL} \biggr) \biggr]^{-0.42} \biggl( \frac{a_sd_p}{\varepsilon} \biggr)^{0.65} \tag{26} \] \[ \begin{align*} \biggl( \frac{\Delta P}{{1 \over 2}\rho_Gu_G^2} \biggr) \frac{d_p}{L} & = 155 \biggl[ \frac{\rho_Gu_G\varepsilon d_p}{\mu_G(1-\varepsilon)} \biggr]^{-0.37} \biggl[ \frac{1-\varepsilon}{\varepsilon(1-\beta_t)} \biggr] \tag{27} \\ \beta_{stat} & =\frac{1}{20+0.9E_O} \tag{28} \\ E_O & =\frac{\rho_Lgd_p^2\varepsilon^2}{\sigma(1-\varepsilon)^2} \tag{29} \\ \beta_t & =\beta_{stat}+\beta_{dyn}=\frac{\varepsilon_L}{\varepsilon} \tag{30} \\ a_s & =\frac{6(1-\varepsilon)}{d_p} \tag{31} \end{align*} \]

なお、ヤコビ行列は、数値微分を使い、連立方程式の解法はGauss-Jordan法（m_lnqgyルーチン）を利用しなさい。気液空塔速度、物性値、充填物代表物性は02_problem.xlsに与えられるものとする。

【注】トリクルベッドでは充填層に液が流れると、充填物表面に液が流れ、その上の隙間にガスが流れる（ガス相連続のとき）。ガス相の圧損（充填層の全圧損）は、固相＋液相の容積割合に影響を受ける。従って、液相の割合を示す液ホールドアップに大きく影響を受けることになる。逆に液ホールドアップも圧損の影響を受け、一般に両者は上のように非線形の関係となる。

【ヒント】
(1) 静的ホールドアップ \( \beta _{stat} \) を(28),(29)から計算
(2) \( \beta _t \) と圧損 \( \Delta P/L \) を仮定（２変数Newton法にする）
(3) (26)式のアンバランス、および(27)式のアンバランスを目的関数とする。
　　（アンバランスがゼロとなるよう収束させることを考える
(4) ヤコビ行列は数値微分により計算
(5) 2x2の正方行列を解くことになる。

練習問題３（上級者用）：多変数ニュートン法による平衡組成の計算法

Lagrange乗数を用いたGibbs自由エネルギーの最小化法(L2982,L2985)により、次の組成をもつ混合気体の、圧力一定のもとでの平衡組成を計算せよ。なお、基礎式（導出などは原典を参照）は次のとおり。

【基礎式】 \[ \begin{align*} \mu_j + \sum_{i=1}^l {\lambda_i \alpha_{ij} } & =0, ~~~ (j=1,n) \tag{32} \\ \sum_{j=1}^n {\alpha_{ij} n_j } - b_j^0 & =0, ~~~ (i=1,l\ ) \tag{33} \\ \mu_j =\mu_j^0+RT\ln p_j & = \mu_j^0 + RT \ln {\biggl( \frac{n_j}{\Sigma n_i} \biggr) } + RT \ln P \tag{34} \\ \end{align*} \]

ここで、
\( \mu_j,(j=1,n) \) は、T,P一定のときの成分ｊの化学ポテンシャル。 \( n \)は化学種の数
\( \mu_j^0 \) は、T,P一定のときの１atmにおける理想気体の化学ポテンシャル[J/mol]（純成分ｊの自由エネルギー \( G_j^0 \) に等しい）
\( P,T,R \) は、それぞれ全圧[atm]、温度[K]、ガス定数[8.31451 J/mol/K]を示す。
\( \lambda_i,(i=1,l\ ) \) は、Lagrange乗数（非ゼロの一定値）で、未知数。 \( l\ \)は元素の種類の数。
\( n_j \) は、混合ガスに含まれる種ｊのモル量
\( \alpha_{ij} \) は、化学種ｊに含まれる元素ｉの量論数
\( b_i^0 \) は、初期モル量から算出した元素ｉのモル量

【初期状態】初期状態は次表のとおり。成分数（化学種）\( n=6 \) 、元素の種類CHONの \( l=4 \)

表１：初期組成
Species Unit Value
1 CO [kmol/s]
2 CO2 [kmol/s]
3 H2 [kmol/s]
4 CH4 [kmol/s] 0.2
5 H2O [kmol/s] 0.6
6 N2 [kmol/s] 0.2
Total [kmol/s] 1
Temp [degK] 1000
Press [atm] 5

なお、各成分の自由エネルギーの計算はすでに定義済みの関数(y_phypror関数）を用いること。

【ヒント】温度、圧力は与えられており、(32)から(34)式の \( n+l \) 個の式があり、未知数は、 出口平衡組成の \( n_j,(j=1,n) \) とLagrange定数 \( \lambda_i,(i=1,l\ ) \) の \( n+l \) 個となり、解ける。 ギブス自由エネルギーは温度のみの関数であり、出口平衡組成が(34)式の対数内にあり、非線形連立方程式となっている。これを複数個の未知数をもつ、Newton法で収束させる。このとき、出口組成が正である範囲を探す。Lagrange定数は非ゼロの制約のみ（負でもよい）。初期値として出口組成は0.1（適当）、Lagrange定数は100（適当、根拠なし）を使う。

先頭に戻る

演習問題の解答

上の演習問題の解答、およびファイルのダウンロードは、こちら（未リンク）で取り扱っています。

先頭に戻る

Literature Cited

引用文献の[Lxxxx]（xxxxは４桁の整数）は、SK-PEOにて管理する連番であることを示しています。

先頭に戻る