トップ > ライブラリ > 技術計算 > 混合・拡散

技術計算：混合・拡散

現在工事中。ひと通りの項目を記述しましたが、誤字・脱字がある可能性があります。また途中でリンク切れなどもあるかもしれませんが、ご容赦願います。順次見直すつもりです。

反応器の性能を予測し、装置のスケールアップするのに必要な装置内混合について以下まとめた。装置内の流れをモデル化することにより、反応成績の予測に役立つとともに、予測精度を高めるために必要な滞留時間分布についてまとめた。

反応器のスケールアップに必要な代表的な理想流れモデルおよび非理想流れモデルの滞留時間分布を示し、これらモデルのパラメータを相互に予測する分散を示した。また実際の滞留時間分布関数をフィッティングする上で必要になる特殊な混合モデルについても言及し、過去事例を紹介する。

【注】数式表示にはMathJaxを利用しています。IE8以下では表示が遅くなる可能性があります。FireFox などIE8以外のブラウザを利用下さい。

先頭に戻る

反応装置内の混合と拡散

化学反応を伴うとき、反応器内部の流体混合の特徴や程度を把握することは非常に重要である。 化学反応は分子レベルのミクロの現象であり、反応を起こす分子の周りの環境に大きく依存する。 こうした反応場の環境を、定性的および定量的に評価するとき、化学工学ではある程度マクロな流体混合を考慮する。 すなわち流体粒子群が反応場に流入して流出するまで、各粒子群がどのような挙動を示すかを評価することにより、 反応場の状況をマクロに把握し、化学反応のミクロ場を推察する根拠を与える。

具体的にいえば、ある装置内の流体粒子の流れ挙動は、粒子の平均滞留時間および滞留時間分布で特徴づけられる混合特性で表現できる。特に化学反応場では滞留時間分布は大きな意味をもち、反応収率や反応生成物に大きな影響を与える。 たとえばモノマーの連鎖反応を考えると、反応器内の滞留時間分布に応じて、分子量分布をもつポリマーが生成してしまう。もちろん連鎖停止反応や連鎖移動反応により分布は変わる可能性があるが、基本的には反応器の滞留時間分布が支配的となる。

気相反応や流速の速い低粘性流体が関与する液相反応では多くの反応器内部の流れは、乱流場に相当し、微小な乱流渦が生成され、空間的・時間的に流れの挙動が変動することになる。乱流渦が発生することにより、拡散速度が見掛け上増加する。これを乱流拡散といい、通常の分子拡散に比べ桁違いに速い。

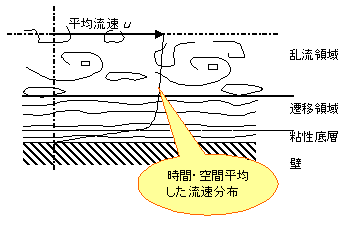
配管内を流体が流れるときの様子を模式的に示すと、図１のように時間・空間平均の流れ方向速度分布は1/7乗則と呼ばれる中心で最大流速をとり、管壁に近づくにつれ次第に遅くなり、管壁近傍で急速にゼロに近づく。

図１：配管内の乱流（模式図）

配管内の乱流領域では乱流渦の生成・消滅が不定期に、場所を問わず起きており、これらを時間・空間平均することで平均的な1/7乗則の速度分布となる。

配管のような空塔内でも流速が速く乱流状態になれば、乱流渦が生成することから、流れ場に何か邪魔もの（充填物、フィルター、スクリーン、あるいは温度計さや管など）があればその下流側に乱流渦が発生し、滞留時間分布に影響を及ぼすことが予想される。

一般に装置の外部形状、特に反応器の外部形状（外見的形状）からその内部の流動状態を推定することは可能であるが、反応器の性能を予測するには精確な滞留時間分布を測定することが必要である。 特に入り出口ノズルの相対的位置、仕切り板、ドラフトチューブ、撹拌翼、バッフルなど内部品の有無やその形状は滞留時間分布に大きな影響を与える。

先頭に戻る

滞留時間分布関数

装置の容積V、容積流量をF、装置の長さL、線速度vのときを考える。また、 時間として平均滞留時間\( \theta_T \) を使い、無次元化した時間\( \theta \)を用いる。 \[ \begin{align*} \theta & = \frac t{\theta_T} \tag{1} \\ \theta_T & =\frac VF = \frac Lv \tag{2} \\ \end{align*} \]

ある装置を考え、流体が定常的に入口ノズルから流入し、出口ノズルから流出する場合を考える。 流体中のある要素（粒子）が、系内に流入してから系外に流出するまでの滞留時間が\( \theta \) と\( \theta + d\theta \) の間にある流体要素の分率を\( E( \theta )d \theta \) として定義する。 この\( E(\theta) \)を滞留時間分布関数(residence time distribution function)または排出頻度関数という。

\[ \begin{align*} \int_0^\infty E(\theta)d\theta = 1 \tag{3} \end{align*} \]

また出口の流出流を考え、流出流中の\( \theta \)もしくはそれより小さい滞留時間をもつ流体要素の分率を\( F(\theta) \) とし、 \( \theta \) より大きい滞留時間をもつ流体要素の割合を\( R(\theta) \)とすると、 \[ \begin{align*} F( \theta ) + R( \theta ) = 1 \tag{4} \end{align*} \]

が成立し、これら定義から次の関係がある。 \[ \begin{align*} \ E(\theta) = \frac {dF(\theta)}{d\theta} = - \frac {dR(\theta)}{d\theta} \tag{5} \end{align*} \]

ここで \(R(\theta)\)を残余濃度曲線(residence time curve)1)という。また\( F(\theta) \) を過渡応答曲線という。

先頭に戻る

滞留時間分布関数の測定法

ある装置の滞留時間分布関数\( E(\theta) \)を測定する方法について考察する。 \( E(\theta) \)を直接測定するのではなく、\( F(\theta) \)や\( R(\theta) \)を測定し、数学処理により\( E(\theta) \)に変換してもよい。

代表的な測定方法は以下のとおり。

過渡応答（またはステップ応答という）は、容積\( V \) の装置に流体の無次元化濃度ゼロの流体が連続的に供給されていて、時刻ゼロの瞬間に無次元化濃度1.0の流体に、流量を保ったまま切り替えるとき、出口で観察される無次元濃度変化を時刻に対してプロットしたものが\( F(\theta) \) になる。 逆に、無次元化濃度1.0の流体が連続的に供給されていて、時刻ゼロの瞬間に無次元化濃度ゼロの流体に、流量を保ったまま切り替えるとき、出口で観察される無次元濃度変化を時刻に対してプロットしたものが\( R(\theta) \) になる。 具体的には、常時水を供給しておき、時刻ゼロで塩の水溶液に切り替え、出口の電気伝導度の時間変化をプロットすることにより、ステップ応答曲線を得ることができる。

δ応答（またはパルス応答という）は、Diracのδ関数で表される濃度パルスを、系に流入する定常流に瞬間的に添加し、出口濃度の時間変化をプロットしたものをδ応答といい、その応答曲線は滞留時間分布関数\( E(\theta) \) となる。 実験的に瞬時に濃度パルスを投入することは不可能であり、平均滞留時間に比べて短い時間でパルスを投入することで、近似的に\( E(\theta) \) を得ることができる。

周波数応答は、ステップ状信号やパルス状信号を入力するのではなく、正弦波状の濃度変動を与えたときの出口の濃度変動を測定する方法である。

上にリストアップした方法以外に、実装置の非定常操作（スタートアップ、シャットダウン、洗浄操作、銘柄切替など）のときのように、原料組成を切り替える操作を行う場合に出口組成を連続的または断続的に分析測定し、分析値を切り替え開始時点からの経過時間でプロットすることによりステップ応答曲線\( F(\theta) \) を得ることができる。

先頭に戻る

典型的な混合モデル

装置内の流れを表す基本的な混合モデルは、両極端なケースとして、混合拡散がないとしたプラグフローモデルおよび混合拡散係数が無限大とした完全混合槽モデルの２つの理想流れモデルがある。 現実の装置内ではこれら両極端な流れモデルではなく、これらの中間的な流れモデル、いわゆる非理想流れ（不完全混合モデル）で表され、有限の混合拡散係数をとる。

装置内の混合拡散の程度により、下に示す理想流れモデルと非理想流れモデルに大別できる。これ以外に特殊な混合モデルとして、装置内をショートパスする流れ、よどみがある流れ、デッドスペースがある流れを場合によっては考慮する必要がある。 \[ \begin{align*} \left\{ \eqalign{ & 理想流れモデル \\ & \left\{ \eqalign{ & プラグフローモデル \\ & 完全混合槽モデル \\ } \right. \\ & 非理想流れ（不完全混合）モデル \\ & \left\{ \eqalign{ & 混合拡散モデル \\ & 槽列モデル \\ & 逆混合モデル \\ } \right. \\ & 特殊な混合モデル \\ & \quad ショートパス、よどみ \\ } \right. \\ \end{align*} \]

非理想流れモデルには、混合拡散モデル(Dispersion Model)、槽列モデル(CSTRs Model)、逆混合モデル(Backmixing Model)の３つがある。 反応工学のところでも述べたように、混合の不完全さを表すパラメータの取り方がそれぞれ違い、混合拡散モデルでは混合拡散係数を、 槽列モデルでは槽列数を、逆混合モデルでは逆流比を、変化させることにより、その滞留時間分布\( E(\theta) \) を調整することができる。逆にいえば、滞留時間分布を測定することにより、その装置の流れの非理想性を表すパラメータを逆算することができる。

反応器のこうした非理想性は、しばしばモックアップ試験装置を用い、滞留時間分布を測定することがある。これにより混合特性を把握し、装置設計に役立てることができる。

先頭に戻る

理想流れモデル

理想流れモデルとして、完全混合槽モデルおよびプラグフローモデルを取り上げる。 完全混合槽モデルでは、拡散係数が無限大であるという前提で理想化している。一方プラグフローモデルでは拡散係数がゼロであるという前提で理想化している。 ここで拡散係数とは分子拡散係数と乱流拡散とを含んでいるとする。 現実の装置ではこれら両極端な理想的モデルでは表現できず、これらの中間的な現実モデルを採用することが多い。非理想流れについては次節で取り上げる。

完全混合槽モデル

完全混合モデルでは、流入する流体は瞬時に反応器内に存在する流体と均一混合し、流入する容積流量と同じ容積流量で流出すると考える。流出する流体の組成も反応器内流体の組成と同じであると考える。

これを定式化する。反応器容積 \( V \) 、入口容積流量 \( F \) 、出口成分 \( C_A \) 濃度 のときの非定常物質収支式は、 反応速度 \( r_A \) とし、次式で表される。定常状態では(1)式左辺がゼロとなり、単純な非線形連立方程式となる。 差分化する必要はない。

\[ \left. \eqalign{ \begin{align*} & V \frac{dC_A}{dt} = FC_{A0} - FC_A + Vr_A \\ & {\rm (IC1) :} \quad C_A =C_{A,\ {\rm ini}},~~ t=0 \cr \end{align*} } \right. \tag{6} \]

ここで左辺は蓄積項、右辺第１項は流入項、第２項は流出項、第３項は反応による生成項を示す。

完全混合槽モデルの基礎式を使い、ステップ応答による滞留時間分布関数\( E(\theta) \) を、以下導出する。 導出に当たり、反応項はゼロとし、次の無次元化を行う。 \[ \left. \eqalign{ \begin{align*} \theta_T & = \frac VF \\ \theta & = \frac t{\theta_T} \\ C_A^* & = \frac {C_A}{C_{A0}} \end{align*} } \right. \tag{7} \]

これら無次元変数を(6)式に代入し整理する。また、時刻ゼロ以前の系内の無次元濃度はゼロ（ステップ応答のとき）であるから、初期条件は時刻ゼロで濃度ゼロとなる。 \[ \left. \eqalign{ \begin{align*} & \frac{dC_A^*}{dt} = (1- C_A^*) \\ & {\rm (IC1) :} \quad C_A^* = 0,~~ \theta = 0 \cr \end{align*} } \right. \tag{8} \]

(8)式を解析的に積分し、初期条件から積分定数を決めることができ、解析解は \[ \begin{align*} C_A^* = 1- \exp(-\theta) \tag{9} \end{align*} \]

となる。ステップ応答法では出口の濃度変化が過渡応答曲線\( F(\theta) \)に等しく、これを(5)式に従って微分することにより滞留時間分布関数\( E(\theta) \)が得られる。 \[ \left. \eqalign{ \begin{align*} F(\theta) & = 1- \exp(-\theta) \\ E(\theta) & = \exp(-\theta) \\ \end{align*} } \right. \tag{10} \]

反応器出口の無次元化濃度の時間変化は(10)式の\( F(\theta) \) で表され、図１の右上がりの曲線となる。時刻ゼロで真水を塩水に瞬時に切り替えたときの反応器出口の塩分濃度の挙動である。 また滞留時間分布関数\( E(\theta) \) は、\( F(\theta) \) を\( \theta \) で微分した(10)式の下の式となり、図１の右下がりの曲線となる。

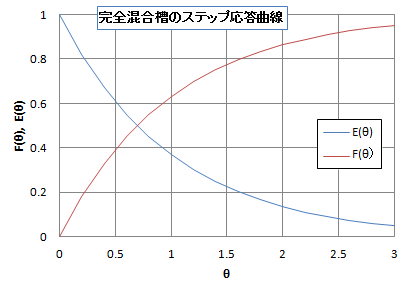
図１：完全混合槽モデルのステップ応答と滞留時間分布

\( E(\theta) \) は、完全混合槽入口に、たとえばインクを一滴垂らしたときの、出口のインクの濃度変化を表している。

先頭に戻る

プラグフローモデル

流れ方向を\( z \) 軸とし、線速度\( u \) で流れる管型反応器で、A成分の一次元非定常物質収支式は次式で表される。

\[ \left. \eqalign{ \begin{align*} & \frac{\partial C_A}{\partial t} + u \frac{\partial C_A}{\partial z} = - r_A \cr & {\rm (IC1) :} \quad C_A =C_{A,\ {\rm ini}}, ~~ t=0 \cr & {\rm (BC2) :} \quad C_A =C_{A,\ {\rm in}}, ~~ z=0 \cr \end{align*} } \right. \tag{11} \] 解析空間として、時間と空間の2次元、偏微分方程式となる。定常状態では左辺第１項の非定常項がゼロとなり、式の形は流入流出のない非定常完全混合槽モデルと同一となる。 完全混合槽をバッチ式反応器として使用したとき、プラグフローモデルの基礎式と同じとなる。ただしプラグフローでは\( u/dz \) という代表時間となる。

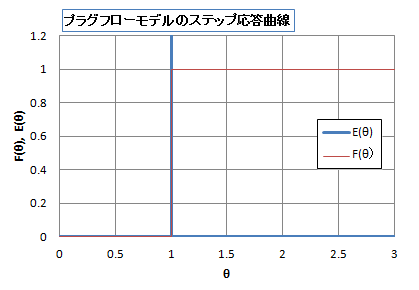
図２：プラグフローモデルのステップ応答と滞留時間分布

プラグフローのときの、ステップ応答曲線\( F(\theta) \) と滞留時間分布関数\( E(\theta) \) を図２に示す。 ステップ応答では滞留時間\( \theta) \) が1.0のときから無次元濃度1.0となり、それ以前は濃度0.0となる。 また滞留時間分布関数はDiracのδ関数がそのまま\( \theta=1.0 \) の時刻に発現している。 δ関数の形（幅はゼロ、高さは無限大、積分すると面積は1.0）が変化していない。

先頭に戻る

非理想流れモデル

非理想流れモデルとして、混合拡散モデル(Dispersion Model)、槽列モデル(Tank in series Model)、逆混合モデル(Backmixing Model)の3つのモデルを取り上げる。

混合拡散モデル

流れ方向を\( z \)軸とし、線速度\( u \)、混合拡散係数\( E_z \) で流れる、長さ\( L \)の反応器を考える。A成分の一次元非定常物質収支式および境界条件（注１）は、次式で表される。

\[ \left. \eqalign{ \begin{align*} & \frac{\partial C_A}{\partial t} = E_z \frac{\partial^2 C_A}{\partial z^2} - u \frac{\partial C_A}{\partial z} - r_A \cr & {\rm (IC1) :} \quad C_A =C_{A,\ {\rm ini}}, ~~ t=0,z=any \cr & {\rm (BC2) :} \quad C_{A0} =C_A(0+) - \frac{E_z}{u} \frac{\partial C_A(0+)}{\partial z}, ~~ z=0,t=any \cr & {\rm (BC3) :} \quad \frac{\partial C_A}{\partial z} = 0, ~~ z=L,t=any \cr \end{align*} } \right. \tag{12} \]

左辺は非定常項、右辺第１項は乱流拡散項、第２項は移流項、第３項は反応項を示す。 【注１】上式で表される入口境界条件(BC2)をDanckwertsの境界条件という。入口に拡散フラックスがあると考える。出口境界条件は\( L \) が十分長いとし、出口の拡散フラックスをゼロとしている。

混合拡散モデルの基礎式を、次の無次元化変数を用い変形する。このとき反応項は反応なしとしゼロとする。 \[ \left. \eqalign{ \begin{align*} \theta & = \frac t{ \theta_T} \\ \theta_T & = \frac Lu \\ z^* & = \frac zL \\ C_A^* & = \frac {C_A}{C_{A,ini}} \\ \end{align*} } \right. \tag{13} \]

これら無次元変数を(12)式に代入・整理すると(14)式が得られる。 \[ \left. \eqalign{ \begin{align*} & \frac{\partial C_A^*}{\partial \theta} = \frac 1{\rm {Pe}} \frac{\partial^2 C_A^*}{\partial z^{*2}} - \frac{\partial C_A^*}{\partial z^*} \cr & {\rm (IC1) :} \quad C_A^* =1.0, ~~ \theta = 0, z^* =any \cr & {\rm (BC2) :} \quad C_{A0}^* =C_A^*(0+) - \frac 1{\rm {Pe}} \frac{\partial C_A^*(0+)}{\partial z^*}, ~~ z^*=0,\theta=any \cr & {\rm (BC3) :} \quad \frac{\partial C_A^*}{\partial z^*} = 0, ~~ z=1.0,\theta=any \cr \end{align*} } \right. \tag{14} \]

ここで、\( \rm{Pe} \) はPeclet数と呼ばれる無次元数で乱流拡散の程度を表す。 【注】通常のPeclet数は反応器の直径を代表長さとして使うことが多いが、(15)式は代表長さとして流れ方向の反応器長さを採用している。 特にBodenstein Numberと呼ぶこともあるが、ここではPeclet数と呼ぶ。 \[ \begin{align*} {\rm {Pe}} = \frac {uL}{E_z} \tag{15} \end{align*} \]

(14)式をパルス応答のδ関数を初期値として積分すると、次の滞留時間分布関数\( E(\theta) \) が得られる5),7)。 \[ \begin{align*} E(\theta)= 2 \exp \biggl[ \frac {\rm Pe}2 \biggr] \sum_{n=1}^{\infty} \frac{ (-1)^{n+1} \delta_n^2} {\biggl[ \delta_n^2+ \biggl( \displaystyle{ \frac {\rm Pe}2 } \biggr)^2 + {\rm Pe} \biggr]} \exp \biggl[ \biggl( - \frac{ (\displaystyle{ \frac {\rm Pe}2 } )^2+\delta_n^2}{\rm Pe} \biggr) \theta \biggr] \tag{16} \end{align*} \]

ここで\( \delta_n \) は、次式の正根で小さい方から\( \delta_1, \delta_2, \dots \)とする。 \[ \begin{align*} \cot \delta = \frac {\delta}{\rm Pe} - \frac {\rm Pe}{4 \delta} \tag{17} \end{align*} \]

【注】文献により、(16)式の式の形が間違っていることがある。文献1), 5)はミスプリがあり、文献7)の表現（（16)式として採用）は正しい。

(16)式を、Peclet数をゼロから50まで変えたときの滞留時間分布関数\( E(\theta) \) を図３に示す。

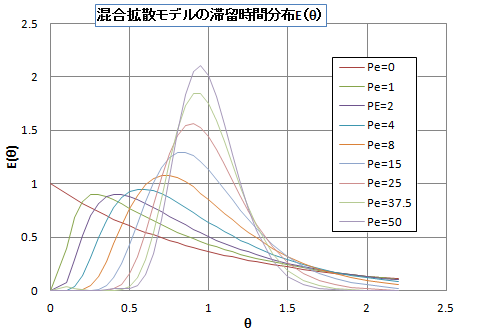
図３：混合拡散モデルの滞留時間分布関数

滞留時間分布関数\( E(\theta) \) の分散\( \sigma^2 \) の計算は、次式の定義から計算できる。 \[ \begin{align*} \sigma ^2 & = \int_0^\infty (\theta - 1)^2E(\theta) d\theta \\ & = \int_0^\infty \theta^2E(\theta)d\theta-1 \tag{18} \end{align*} \]

"closed vessel"のときの滞留時間分布関数(16)式から分散を求めると、 \[ \begin{align*} \sigma ^2 & = \frac 2{\rm Pe} \biggl[1- \frac 1{\rm Pe} \Bigl(1-\exp (- {\rm Pe}) \Bigr) \biggr] \tag{19} \end{align*} \]

となる。Peclet数が大きいとき、［ ］内は1.0となり、分散は \( 2 / {\rm Pe} \)となる。

先頭に戻る

槽列モデル

槽列モデルでは、反応装置を等しい容積の完全混合槽モデルに仮想的に分割し、これらが直列に接続されているとする。今、全反応器容積 \( V \)を\( N \)等分したとき、第j番目の槽の非定常物質収支式は次式で表される。定常状態では、差分化された非線形連立方程式系を構成している。

\[ \left. \eqalign{ \begin{align*} & \frac VN \frac{dC_{A,j}}{dt} = FC_{A,j-1} - FC_{A,j} + \frac VN r_{A,j}, ~~ (j=1,N) \cr & {\rm (IC1) :} \quad C_{A,j} =C_{A,j,\ {\rm ini}},~~ t=0 , (j=1,N) \cr \end{align*} } \right. \tag{20} \]

ここで左辺は非定常蓄積項、右辺第１項は流入項、第２項は流出項、第３項は反応項である。

反応項をゼロとし、先の完全混合槽と同様に無次元化を行う。

\[ \left. \eqalign{ \begin{align*} \theta_T & = \frac V{NF} \\ \theta & = \frac t{\theta_T} \\ C_{A,j}^* & = \frac {C_{A,j}}{C_{A,0}} \end{align*} } \right. \tag{21} \]

これら無次元変数を(20)式に代入し整理する。また、時刻ゼロ以前の系内の無次元濃度はゼロ（ステップ応答のとき）であるから、初期条件は時刻ゼロで濃度ゼロとなる。 \[ \left. \eqalign{ \begin{align*} & \frac{dC_{A,j}^*}{dt} = (C_{A,j-1}^*- C_{A,j}^*) \\ & {\rm (IC1) :} \quad C_{A,j}^* = 0,~~ \theta = 0 \cr \end{align*} } \right. \tag{22} \]

\( j=1 \) のとき上式を解析的に積分し、初期条件から積分定数を決めることができ、解析解は \[ \begin{align*} C_{A,1}^* = \frac {C_{A,1}}{C_{A,0}} = 1- \exp(-\theta) = F_1(\theta) \tag{23} \end{align*} \]

となる。j=2のとき(22)式は、次のように非同次の微分方程式となる。 \[ \begin{align*} & \frac{dC_{A,2}^*}{dt} + C_{A,2}^* = C_{A,1}^* \tag{24} \end{align*} \] 解析解は、 \[ \begin{align*} C_{A,2}^* = \exp(-\theta) \int_0^\theta C_{A,1}^* \exp(\theta) d\theta \tag{25} \end{align*} \] となる。(23)式を代入し、積分すると、\( C_{A,2}^* \) が得られる。 \[ \begin{align*} C_{A,2}^* = 1 - \exp(-\theta) (1+\theta) \tag{26} \end{align*} \] これを第Nセルまで繰り返す。 \[ \begin{align*} C_{A,N}^* = 1 - \exp(-\theta) \Bigl\{ 1 + \theta + {\theta^2 \over 2!} + \cdots + {\theta^{N-1} \over (N-1)! } \Bigr\} \tag{27} \end{align*} \] ここで、\( \theta \)の定義で、(21)式の平均滞留時間\( \theta_T \) はひとつのセルの容積の滞留時間を基準としており、反応器全体の容積に対する平均滞留時間を用いると、上式の\( \theta \)の代わりに\( N\theta \)を使う必要がある。

ステップ応答法では出口の濃度変化が過渡応答曲線\( F(\theta) \)に等しく、これを(5)式に従って微分することにより滞留時間分布関数\( E(\theta) \)が得られる。 以上のことから、槽列モデルの\( F(\theta) \)と滞留時間分布関数\( E(\theta) \)は、全反応容積基準の無次元時刻 \( \theta = {tF \over V} \) を用いると次式となる。 \[ \left. \eqalign{ \begin{align*} F(\theta) & = 1- \exp(-N \theta) \sum_{n=1}^N \frac {(N\theta)^{n-1}}{(n-1)!} \\ E(\theta) & = \frac {N^N}{(N-1)!} \theta ^{N-1} \exp(-N \theta) \\ \end{align*} } \right. \tag{28} \] 槽列数 \( N \)を変えたときの滞留時間分布関数を図４に示す。

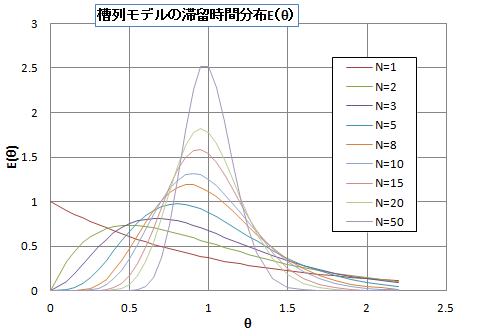
図４：槽列モデルの滞留時間分布関数

槽列モデルの分散は、(18)式（下式）を用いて、 \[ \begin{align*} \sigma ^2 & = \int_0^\infty \theta^2E(\theta)d\theta-1 = \frac {(n+1)n}{n^2} -1 = \frac 1n \tag{29} \end{align*} \] となる。

先頭に戻る

逆混合モデル

図５：逆混合モデルの概要

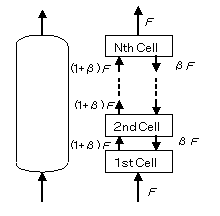
逆混合モデルでは、図５に示す反応容積\( V \) の反応器を \( N \) 等分し、分割された槽は完全混合槽とみなし、各槽には下流側からの逆方向流れ\( \beta F \) を考慮し、流れ方向は逆流を加味した\( (1+\beta)F \) 流量で流出するモデルである。 第１槽目入口および第 N槽目出口の流量は、\( F \) としている。ここで\( \beta \) は逆流比である。

全反応器容積を N等分したとき、第ｊ番目（j=2～N-1）の槽の非定常物質収支式は、逆流比\( \beta \) としたとき、次式で表される。 第１槽、第 N槽では右辺係数が少し違う。定常状態では係数行列がTridiagonal Matrixとなっており、差分化された連立非線形方程式系を構成している。

\[ \left. \eqalign{ \begin{align*} \frac VN \frac{dC_{A,1}}{dt} & = FC_{A,0} - (1+\beta)FC_{A,1} + \beta FC_{A,1} \cr & + \frac VN r_{A,1}, ~~ (j=1) \cr \frac VN \frac{dC_{A,j}}{dt} & = (1+\beta)FC_{A,j-1} - (1+2\beta)FC_{A,j} + \beta FC_{A,j} \cr & + \frac VN r_{A,j}, ~~ (j=2,N-1) \cr \frac VN \frac{dC_{A,N}}{dt} & = (1+\beta)FC_{A,N-1} - (1+\beta)FC_{A,N} \cr & + \frac VN r_{A,N}, ~~ (j=N) \cr {\rm (IC1) :} \quad C_{A,j} & =C_{A,j,\ {\rm ini}},~ t=0 , ~~(j=1,N) \cr \end{align*} } \right\} \tag{30} \] 左辺は非定常蓄積項、右辺第１項は上流からの流入項、第２項は上流および下流への流出項、第３項は下流からの流入項、第４項は反応項である。

定常時の逆混合モデルは、離散化（差分化）した混合拡散モデルと式の形が極めて類似している（第ｊ槽の収支式は、j-1,j,j+1の前後３つの槽の濃度に依存している）。

多段気泡塔で段数 N段で、各段内は拡散モデルPeに従い、段間では逆混合比βの逆混合モデルに従うときの分散の解析解がNishiwaki et al.8,9)により与えられている。さらに段内を完全混合槽とみなす（Pe=0）と N段で逆流比βの逆混合モデルの分散は、次式のようになる。 \[ \begin{align*} \sigma^2 & = (1+\beta)^{1-N} \biggl[ \beta^{N-1} + 2\beta^{N-2} \Bigl( \frac {N-1}{N} \Bigr)^2 \cr & + \sum_{j=2}^{N-1} \beta^{N-j-1}(1+\beta)^{j-2} \Bigl\{ j-1+2(1+\beta) \Bigr\} \Bigl( \frac {N-j}N \Bigr)^2 \biggr] \tag{31} \end{align*} \]

一方、反応器全長\( L \)、分割数\( N \)、逆流比\( \beta \)のとき、逆混合モデルのパルス応答の分散を、混合拡散モデルの分散と等しいとすると、次式が得られる1)。 \[ \begin{align*} \frac 1{\rm Pe} = \frac {E_z}{uL} = \frac N{2(N-1)^2}+\frac {\beta} {N} \tag{32} \end{align*} \]

(31)式と、(32)+(19)式とで計算した分散はNが十分大きいとき(N>10)、10%以下の誤差はあるがほぼ一致する。

先頭に戻る

特殊な混合モデル

滞留時間分布が合うように、理想流れモデルや非理想流れモデルを適用するが、反応器内部の特殊性によりこれらモデルだけで滞留時間分布を合わせることができない場合がある。 混合モデルを精度良く構築しないと、反応シミュレーションなどを実施したとき、信頼性や精度を損なう恐れが高い。

図６：特殊な混合モデル

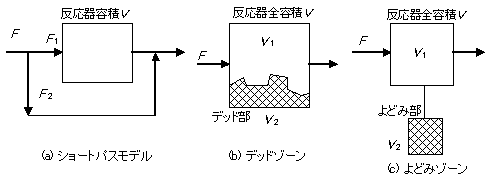
モックアップ装置から得られたパルス応答曲線やステップ応答曲線から滞留時間分布を理想流れや非理想流れモデルだけでフィッティングしようとすると、旨くフィッティングできない場合がある。 たとえば出口濃度がTailingを起こし、なかなか下がらない場合がみられる。こうした現象は、図６に示す特殊な混合モデルを導入することで解決する場合がある。

ショートパス

ショートパスモデルでは、全入口流量 \( F \) のうち、\( F_1 \)の流量が容積\( V \)の反応器へ仮想的に流れ、 残りの流量 \( F_2=F-F_1 \) が仮想的なバイパスを通る（ショートパスする）と考える。

したがって全体の出口濃度の時間変化を考えると、反応器を通る流れは本来の混合モデル（理想流れまたは 非理想流れ）で表され、ショートパスする流れは時刻ゼロの時点（平均滞留時間はゼロであるから）で、 入口に投入した組成が、流量割合に応じてすぐに出口に排出される。

またショートパスが存在するとき、ショートパスする流量に相当する反応器内部の容積が一部死んでいる（機能しない）と考えられ、デッドスペースを同時に考慮することが多い。

Choletteらのモデルでは、反応容積\( V \) を完全混合部分\( V_b \)とよどみ部分\( V_d \)とに分け、流体を主流\( F_1 \) と 分岐流\(F_2\) とに分けると、\( F(t) \)、\(E(t) \) は次式で与えられる11)。 \[ \begin{align*} F(t) = 1- \frac 1{t_b} \frac {V_b}F \exp \biggl(-\frac {t}{t_b} \biggr) \tag{33} \cr E(t) = \frac 1{t_b} \frac {F_1}F \exp \biggl( -\frac {t}{t_b} \biggr) + \frac {F_2}{F} \delta ( t ) \tag{34} \end{align*} \]

ここで、\( t_b=V_b/F_1 \)、\( \delta(t) \)はデルタ関数である。なお上式にはよどみによる効果は無視している。

ショートパスを考慮するとき、その程度を表すパラメータは、流量比 \( F_2/F \) となる。(34)式第１項は主流の完全混合槽の寄与を、第２項はショートパスによる寄与を表している。

先頭に戻る

デッドスペース

先のショートパスのモデルと同様であるが、反応器の全容積 \( V \) のうち、正常に機能する容積 \( V_1 \) と、デッド部の容積 \( V_2 = V - V_1 \) とを考え、入口から流入する流れは \( V_1 \) 部のみに流れるとみなす。

デッドスペースを考慮するとき、その程度を表すパラメータは、容積比 \( V_2/V \) となる。

先頭に戻る

よどみ

よどみモデル(Stagnant Model)は、図６の(c)で示すように、反応器内部に容積 \( V2=V-V_1 \) のよどみ部を考慮する。よどみ部(Stagnant region)では反応器本体部 \( V_1 \) との物質移動を考慮する。

よどみを考慮するとき、その程度を表すパラメータは、本体とよどみ部との間の物質移動係数 \( k_m \) となる。

本体とよどみ部との物質移動速度 \( N_m \)は、次式で表される。 \[ \begin{align*} N_m = k_m A ( C_1 - C_2 ) \tag{35} \end{align*} \]

ここで、\( A \) は本体とよどみ部との界面積、\( C_1 \) は本体側の成分濃度、\( C_2 \)はよどみ部側の成分濃度である。 反応器シミュレーションを行う場合には、本体側とよどみ側とでそれぞれ収支式を立て、両方の収支式に(35)式の物質移動項を考慮する。

フィッティング用のパラメータとして物質移動係数 \( k_m \) ではなく、物質移動容量係数 \( k_mA \) とすることも可能である。

Westerterpら12)は本体側を混合拡散モデルとしたときの、よどみを考慮した基礎式を導出している。

先頭に戻る

過去の解析事例

過去の事例

ある反応器の滞留時間分布の測定データから、その反応器の混合モデルを解析した。反応器本体側は混合拡散モデル＋完全混合モデルの組み合わせモデルを採用し、混合拡散部分によどみモデルを適用した。 混合拡散モデル部分のPeclet数を変えたときの出口濃度の時間変化を、計算値と実測値とで比較した。比較の結果を図７に示す。

図７：よどみモデルを適用した事例

図から、実測値の◇プロットは、後半のTailingが見られる。よどみモデルを適用することによりTailingを旨くフィッティングできていることがわかる。 図には示していないが、よどみモデルを考慮しない場合には、逆Ｓ字部分がほぼ対称となり後半のTailing部分のフィッティングは良くなかった。

図７は、物質移動係数をある値に固定し、混合拡散係数を変えてフィッティングしている。よどみの物質移動係数または混合拡散係数のどちらを合わせるかは、事前にケーススタディを実施しており、ともに最善となる値を選択している。 得られている測定データを解釈する上で最適値を選んだが、これら値の物理的な正確さには多少疑問が残るものの、ある程度の目安にはなる（他の検証手段により物理的な妥当性を判断する必要がある）。

先頭に戻る

Literature Cited

関連ファイルのダウンロードは、こちら（未リンク）で取り扱っています。

先頭に戻る