トップ > ライブラリ > 技術計算 > 反応工学

技術計算：反応工学

現在工事中です。

取り敢えず繋がりましたが、まだまだ未完成（これからも更新する予定）です。

【注】数式表示にはMathJaxを利用しています。IE8以下では表示が遅くなる可能性があります。FireFox などIE8以外のブラウザを利用下さい。

先頭に戻る

反応工学

化学品を製造するプラントでは、原料を反応させて製品を得る化学反応操作を実施している。このとき反応を行わせる装置を反応装置または反応器といい、反応器を解析・設計する工学分野を特に反応工学といっている。 化学製造プロセス内の反応器は心臓部であり、新規開発プロセスでは効率の良い反応条件の探索や反応器の開発が主眼となって研究開発が実施される。

工業的に利用される反応器の様式の分類は、別のところの反応器の分類（未完）で行っているが、反応の起こる相（気相、液相、固相）と反応器の形状（反応器内流れ）による分類がなされている。

ここでは、反応器開発に的を絞り、スケールアップの手順、反応速度解析、流れ・混合の影響など一般的な話題を提供する。反応器は他の単位操作（蒸留、吸収、撹拌などなど）と異なり、一般理論で系統的に解析することが困難であり 個々の反応毎に取り扱う物質が違うことにより、一品毎の設計となることが多い。スケールアップに当たっての統一理論はなきに等しく、まさに過去の経験と感性の世界となる。

先頭に戻る

スケールアップの手順

本章は、化学工学会・人材育成センター主催の「反応器の設計」セミナーで用いたテキスト（2007年版）の液相反応器部分を加筆・修正し、ウェブ用に記述し直したものです。

プロセス開発のステップ

液相反応器に限らず、一般に化学品を製造するプロセスの開発は、表１に示すように、目標とする化学品が現に存在するまたは想定されることが前提となり、ステップを踏んで行われる。最終目標である商業化を達成するため、プロセス開発（R&D：Research and Development）はできるだけ早く（スケジュール）、速く（スピード）、また安く（経済コスト）行う必要がある。製造プロセスとして見たとき、競争力のある製品を生産できるばかりでなく、プロセス自体も合理的に組み立てなければならない。化学プロセスの中で反応器は心臓部であり、もっとも力を入れて開発に取り組むべき対象のひとつと言える。

以下、反応器の装置規模ごとに、スケールアップする際の要点を述べる。

表１：化学プロセスの開発ステップ1)
開発のステップ スケール 主要開発課題
① 目標設定・事前評価 ・現状の問題点の認識
・改善案の着想
・特許、文献、社内情報の調査
② 探索研究 (R-stage) ラボスケール ・着想の具体化
・ラボテストの実験計画策定
・ラボテストの実施
・ラボデータの解析（反応機構、反応速度解析、相関など）
・実験計画へのフィードバック
・特許申請
・ベンチ・パイロット装置の試設計
③ 第１次評価 ・製造技術の評価
・製造コストの評価
・事業計画・開発計画の策定
・特許状況の確認
④ 開発研究 (D-stage) ベンチ・パイロットスケール ・テスト装置の運転、データ採集
・運転データの解析・評価（反応速度解析など）
・各ユニットの詳細設計条件の確認と最適化 (シミュレータ作成、ケーススタディ、スケールアップ因子の抽出）
・製品品質の確認、サンプル出荷
・商業化装置の基本設計
－プロセス設計基本条件の策定
－基本物性の収集・整備
－プロセスフローシーティング
－物質収支・熱収支
－機器設計、スケールアップ
－原料、用役消費量の試算
－建設コスト見積
－製造原価試算
－運転指針作成
－安全・環境面の検討
⑤ 第２次評価 ・製造技術の評価
・製造コストの評価
・安全・環境面の評価
・事業性・採算性の確認
⑥ プラント建設 商業化スケール ・詳細設計
・官庁、法規申請
・機器・工事発注、調達、検査、輸送
・建設工事
・試運転計画
・運転ＳＯＰ作成
⑦ 試運転・営業運転 ・試運転データの採取
・試運転データの解析
・シミュレータチューニング
・プロセス性能解析
・製品品質の解析

先頭に戻る

ラボスケール

図１：スケールアップ倍率

ラボ（実験室）スケールでは、試験管、ビーカー、フラスコなどのガラス器具で反応器を組み立てることが多い。反応温度や反応圧力により、オートクレーブを用いることもある。ラボスケールの反応器は、そのままの形状でスケールアップ（幾何学的相似則が適用される）され、商業化スケールの反応器となることが多々あり、将来の姿をイメージして、ラボスケールの反応器の形状を慎重に決める必要がある。

ラボスケールの実験は、反応原料（触媒を含む）を仕込み、所定の温度・圧力に設定し、所定時間だけ反応を進行させた後、サンプリングし、成分分析を行う。このように反応操作は基本的に定温・定圧のバッチ操作となることが多い。

実験の主目的は、目的とする製品を製造するための、最適な反応条件（温度、圧力、触媒量、滞留時間など）を探索することであり、得られた実験データ（時間と反応物濃度）から、反応機構を推定し、反応次数および反応速度定数を最適化により求め、反応条件から反応成績を精度良く推定できる相関式（真の反応速度）を作成することである。

ラボスケールの反応器は、プラグフロー型反応器または完全混合槽型反応器(CSTR: Continuous Stirred Tank Reactor)のような理想流れの反応器として取り扱える場合が多い。実験データを整理・解析するとき、こうした反応器のモデリング技術を必要とする。

気相反応に見られるラジカル素反応のように反応器形式に依存しない真の反応速度を求めることは一般に困難であり、液相反応のときは、真の反応速度にできるだけ近い総括の反応速度を求めることになる。反応速度が求められると、反応器モデルとシミュレータを用いベンチ装置またはパイロット装置の反応器を設計することになる。このとき将来の商業スケールの反応器の形式がほぼ決定される。すなわち、
－連続反応装置とするか、バッチ反応装置とするか
－CSTR型にするか、プラグフロー型にするか、あるいは中間型にするか
を判断しなければならない。判断するに当たり、商業プラントの生産規模、反応条件、要求される製品品質、経済環境などさまざまな制約を勘案し、高度で総合的な判断が要求される。

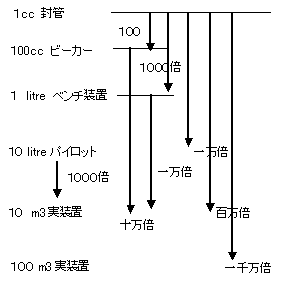
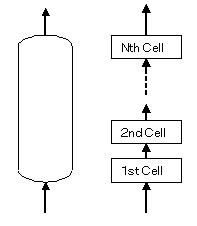
ラボからベンチ・パイロットへ、ベンチ・パイロットから商業プラントへのスケールアップに当たり、反応器のスケールアップ倍率（図１参照）は、一般に数百から一万倍程度が採用される。スケールアップ倍率は、反応器形式、反応の複雑さ、反応速度式の信頼性、反応器モデルの複雑さやモデルの精度に依存し、ベースとなる小規模テストの信頼度に大きく左右される。

先頭に戻る

ベンチ・パイロットスケール

図２：幾何学的相似則

ベンチ装置あるいはパイロット装置の試験では、ラボスケールで作成した最適反応条件を再現できるか、製品品質上の問題はないか、副反応による微量成分の生成や蓄積がないか、長時間連続運転による変動（触媒の劣化、コーキング、腐食）がないか、安全・環境面の問題はないかなどを確認する。また構成する機器毎の性能を確認したり、装置設計に必要なデータの取得を行う。

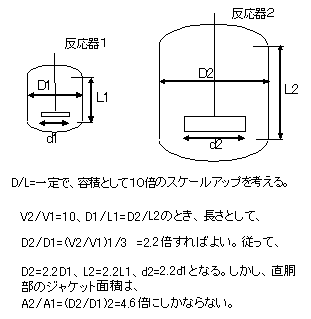
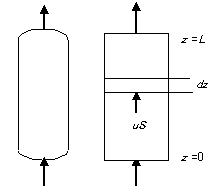
ベンチ・パイロットスケールの反応器は、商業化スケールの一歩手前の規模であり、商業器を設計するときは幾何学的相似則に基づきスケールアップされる（図２参照）。このとき反応器形式をベンチ・パイロット装置と全く異なる形式とすることは通常行わない。幾何学的相似則に従わない諸量（例えば伝熱面積、空塔速度）を、どこまで満足させるかが反応器の設計者の「腕の見せどころ」となる。

「反応器サイズを支配する因子は何なのか」を、ラボやベンチ・パイロット装置の設計を通して、把握することが肝要である。反応速度（容積）なのか、伝熱速度なのか、撹拌速度なのか、物質移動速度なのかを見極めることが重要となる。反応の起きている器（反応器）を、物理・化学的に単純化し、こうした支配因子を適切にモデル化することが要求される。しかも、そのモデルが現象を忠実に再現していることが要求される。

先頭に戻る

商業化スケール

ファーストプラントとなる反応器（１号機）は、ベンチ・パイロット試験を通じて、プロセス工学的な面の欠点や欠陥はほとんどクリアされているが、規模が大きくなることによるリスクを考慮し、設計されなければならない。

２号機以降の設計では、スケールアップ手法は確立しており、マイナーなブラッシアップ程度の改良で済むことが多い。逆に、メジャーな改良を加えるときは、小規模スケールに戻り、追試・再試験を行うなど始めからやり直す。

規模が大きくなることにより、逆混合流れ、副反応生成物の蓄積、流れの偏流・分散不良、デッドスペースの生成、およびネガテクノロジーと呼ばれる問題（Negative Technology：閉塞・固結・フォーミング・飛沫同伴）などプロセス上のリスクがあり、設計段階で前もって対策を講じておく必要がある。また機械としての反応器に関わるリスクや予測不可能なリスクもある。想定可能なリスクは、設計段階であらゆる手段を講じ対策を施しておく。

先頭に戻る

スケールアップの留意点

スケールアップに伴う課題のひとつに、規模が大きくなることの影響がどこに出現するかを見極めることである。

例えば、小さいスケールではA/V（熱移動面積/反応器容積の比）は、先の図２に示したように大きく取れ、ラボ装置やベンチ装置で除熱・加熱を工夫する必要はない。小さい装置では放熱による熱ロスにより発熱反応では除去する熱量が相対的に小さくなり、伝熱面積は小さくても温度コントロールは比較的容易になる。もちろん、逆に吸熱反応では熱ロス分を含めた熱量を供給しなければならず、伝熱面積が大きくなる。

大型の特に商業規模の反応器になると、ベンチ・パイロット装置と幾何学的相似則に従って伝熱面積をとると、同じA/Vとはならない。そこで同じA/Vとなるよう、幾何学的相似則は一部崩れることになるが、反応器内に伝熱面積を追加したり、対流伝熱以外の除・加熱方法を工夫するなど対策を施すことになる。

例えば撹拌槽型反応器のとき、熱収支式および除去熱量Qは次式となる。 \[ \begin{align*} \rho c_p \frac {\partial T}{\partial t} & = F_{\rm in}c_{p,{\rm in}}T_{\rm in} - Fc_pT-Q-r \Delta H \tag{1} \\ Q & =UA(T-T_w) \tag{2} \end{align*} \]

図３：反応熱の除去方法3)

除去熱量Qは、総括の伝熱係数U、伝熱面積Aおよびプロセス流体の温度Tおよび除熱媒体の温度Twから求められる。ジャケットやコイルを使うとき総括伝熱係数Uは、運転条件すなわち撹拌レイノルズ数やプラントル数が決まれば自ずと決まってしまい自由度は少ない。また、除熱媒体温度Twも、冷却水やチラー水、冷媒を用いるなど工業的規模の設計では制約があり自由度は少ない。従って、残された方法は伝熱面積Aを如何に増加させるかということになる。

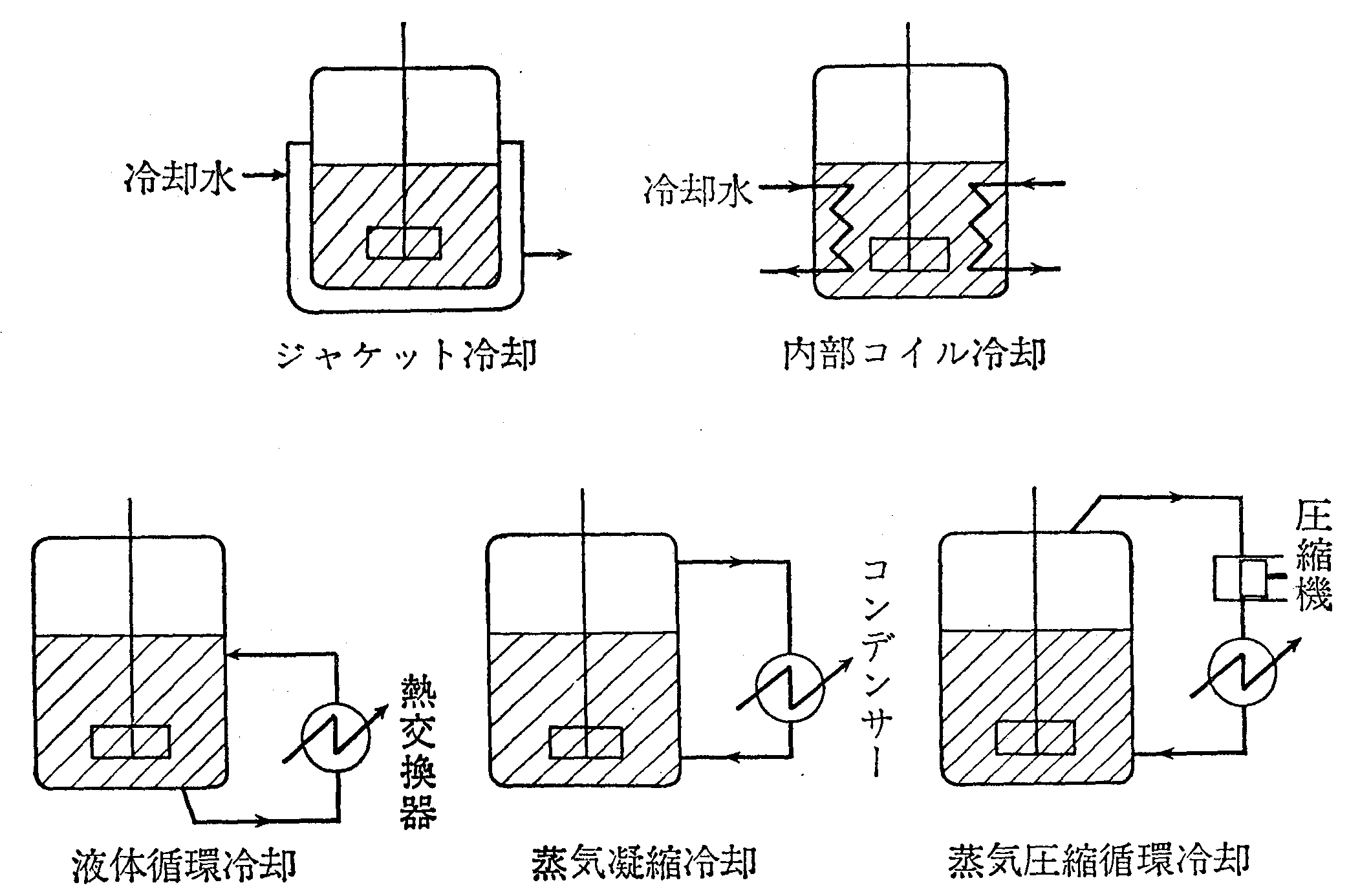
伝熱面積Aを確保し、熱除去量を増やすため、図３に示す外部循環型熱交換器を採用したり、リフラックスコンデンサーを用いた反応熱除去など、熱除去方法を工夫することになる。

先頭に戻る

反応器のスケールアップ

図４：速度解析とスケールアップ

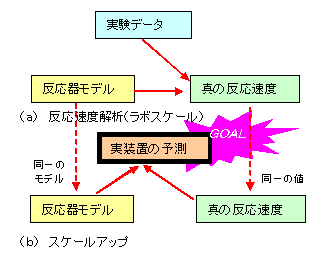
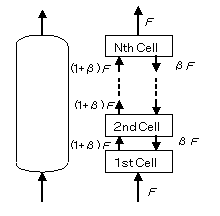
図４(a)に示すように、ラボスケールでは、実験データ（反応条件と反応成績）と反応器モデル（通常、理想流れモデルとなる）を用いて、真の反応速度を最適化し、反応速度定数を求める。図の３つの頂点から出る矢印の向きは、真の反応速度の方向を向いている。一方、ベンチ・パイロットスケール、商業化スケールとスケールアップするとき、図４(b)に示すように、ラボと同一の反応器モデルを採用し、またラボで求めた同じ反応速度定数を採用し、反応器の反応成績を予測することを行う。矢印の向きは今度は実装置の予測の方向を向いている。

このように反応速度解析とスケールアップには、３つの頂点は同じでベクトルの向いている方向が異なるという類似性がある。確実な反応器挙動の予測を行い、スケールアップを成功させるには、基盤となる反応器モデルと反応速度を含めた反応モデルの両方の信頼性を高めることが大切である。また、反応モデルを反応器モデルに組み込み、これを解くシミュレーション技術も、スケールアップに必要な基盤技術のひとつである。

反応器をスケールアップするとき、次の３つの技術が必要となる。

反応器のスケールアップとは、「反応モデルを含む反応器モデルを精度良く構築し、このモデルに則って規模を拡大すること」といえる。スケールアップを成功させるには、真の反応速度を測定し、反応器モデルのパラメータを精度の良いまた適用範囲の広い相関式で構築することに尽きる。知見が不足しているところを、小スケール規模のテストでデータを取得し、確認し、補うことが成功への近道となる。

次節以降に、反応器設計で避けて通ることのできない以下の項目について解説する。

先頭に戻る

反応速度の解析

反応モデルの構築の詳細は、こちら（未リンク）を参照されたい。以下、簡単に述べる。

ここで取り上げる「反応速度の解析」には、反応モデルの構築（反応経路の確立）、反応次数の決定、反応速度式の定式化、反応速度定数の最適化を含む。ラボ実験のデータを用い、簡単な反応器モデルを採用し、反応器シミュレータを用いて反応速度定数を最適化して求める。このとき物質移動・熱移動、流体の混合などの物理的な要因を排除した真の反応速度を求めることが大切である。液相反応で真の反応速度を求めることは前にも述べたように不可能に近く、総括の反応速度を求めることになる。また、ラボ装置の混合モデルは理想流れモデルとなることが多い。混合モデルは次節で取り扱う。

反応モデル

ラボ実験あるいはベンチ実験のように比較的小規模スケールの試験装置で得られた実験データの整理、解析および反応速度式の構築に至るまでの手順を考える。言うまでもなく、事前に整理や解析に必要な物性の推算方法を確立しておく必要がある。

反応モデルとは、原料Ａ、Ｂ、･･･が製品Ｐに至るまでの、中間原料、反応副生成物、反応媒体などを含め、考えられる反応経路を、化学反応式として表したものである。また副反応のように、製品品質や原料原単位に影響を及ぼす反応式も含め、反応モデルを構築しなければならない。反応モデルに組み込む反応式は、少なくとも元素のモルバランスが取れている必要があり、反応に関与する物質の分子量がわかっている必要がある。また総括の反応だけでなく、逐次反応であるとか並列反応であるとか、平衡反応であるなどの情報も分かっていれば、反応モデルに考慮する。

原料成分Ａ、Ｂは、つぎの単一反応（複合反応のときもある）により製品Ｐ、副生成物Ｑになると考える。 \[ \begin{align*} aA ~ + ~ bB ~ \longrightarrow ~ pP ~ + ~ qQ \tag{3} \end{align*} \] この反応の反応速度ｒ（単位容積当たりの反応モル数）は、Ci を成分i のモル濃度とすると、 \[ \begin{align*} r & =kC_A^mC_B^n \tag{4} \\ k & =k_0 \exp \biggl( - \frac E{RT} \biggr) \tag{5} \end{align*} \] で表される。m 、n は成分Ａ、Ｂの反応次数、ｋは反応速度定数で、通常(5)式のようにArrhenius式で表される。k0は頻度因子、E は活性化エネルギーである。

反応速度定数の最適化に先立ち、文献等で既存の速度式あるいはポイントの速度定数を調査する。一般にこれらデータは公表されていないことが多い。類似成分の反応や同じ形式の反応（酸化反応、還元反応、置換反応、エステル化反応など）で、反応次数や反応速度定数について、公表された文献などの情報をできるだけ調査しておくと、最適化時に未知数を減らすことができ、解析のスピードアップに役立つ。

反応モデルを構築し、これを反応器モデルに組み込み、物質・熱収支を解くツールを構築することで、反応器のシミュレーションが可能となる。反応モデルに組み込む反応はいわゆる「素反応」でなくても良く、液相反応のときには反応の律速段階を表す総括の反応が通常使われる。あまりに多くの反応を組み込むと、反応器シミュレーションに負荷（計算時間、メモリ）がかかり、現実的なツールとならないことがある。

先頭に戻る

装置形状および実験条件

反応速度を解析するとき、反応試験に用いられた反応器の装置形状を知っておく必要がある。特に内部構造が複雑なものについては製作図を入手する。反応器内部の流れをモデル化するとき、デッド（滞留）部となりそうな箇所がないか、ショートパス流れを生成するようなノズル位置にないか、入口ノズルから流体が均一に分散するか、槽内の偏流は考えられないか、など装置内のフローパターン（流れの様子）をイメージし、図面をチェックする。また内部品があるとき、撹拌翼の形状、翼から吐出される流れの方向、バッフルの有無、バッフルの固定のし方（壁との隙間の有無）、翼と槽、翼と底面、翼と液面などの相対位置を把握し、混合モデルの選択の参考とする。

実験は連続流通実験かバッチ実験か、等温反応か断熱反応かを明らかにしておく。また固体触媒を用いるときは、その触媒の形状、寸法、寸法の分布、履歴（再生したもの、再生条件、新品、ある程度使い込んだもの）など触媒の製造・調整方法も含め、実験データを整理する。気固、液固反応のときは、固体触媒表面への吸着速度や表面からの脱着速度が反応の律速段階となることもあり、このようなときは触媒の比表面積の違いにも留意する必要がある。

先頭に戻る

データの健全性

反応速度解析に先立ち、得られた反応速度データの健全性をチェックする。反応式がわかっている場合は成分の収支や元素の収支が取れているか、連続流通試験の場合には入口と出口とで重量基準の全体の収支がとれているか、バッチ試験のときには仕込み時と終了時とで重量基準の収支がとれているか、反応熱・放熱を考慮して熱収支がとれているかを確認する。アンバランスの大きいデータは解析から除外する。

また表計算アプリケーションを用い、実験で得られた反応条件や反応成績をプロットし、全体の傾向に矛盾がないか（例えば、実験データから算出される速度定数ｋを1/Tでプロットし、ほぼ直線で近似できるか）をチェックしておく。また傾向が逆転していたり飛び離れていたり、データに異常があるときには、再現実験を行い確認することもある。

反応実験データに、データ点の偏り（採取したデータが、高転化率側に偏っていたりしていると、低転化率側の推算精度が劣る）がないかもチェックする。回帰分析や最小二乗により最適化フィッティングして求めた速度定数は、実験データの内挿領域でしか適用することはできない。外挿領域にならないよう、できるだけ広範な実験データを採取することを心掛ける。

測定値には、センサーのもつ誤差（測定の時間遅れを含む）、サンプリングの方法、測定・分析の誤差、天候・気象条件による誤差、実験担当者の人的誤差など多くの誤差が積み重なっている。これら内包する誤差要因を念頭に入れて、データを整理・解析する必要がある。こうしたデータの信頼性を勘案し、解析結果が妥当なものかどうかを評価し判断しなければならない。また誤差分析などを実施し、測定値をできるだけ精度良くとれるよう実験計画や設備計画を立て、測定方法の改善を行うこともある。

先頭に戻る

混合モデルと反応速度

次に反応速度データを採取したラボ装置やパイロット装置の混合モデルを作成し、反応速度定数を求めることを考える。装置内の混合モデルと反応速度定数とはお互いに密接に関連しており、混合モデルに依存しない真の反応速度定数が得られるようにデータ採取や装置選定を行う必要がある。一方装置規模の大小を問わずあらゆる反応器に対して、混合モデルを適用しないと反応速度定数が得られない。反応速度を求める実験は、ラボ装置で行うことが多く、プラグフローモデルや完全混合モデルのような理想流れモデルを仮定することで十分な場合が多い。また実験条件や反応器形状も、仮定した混合モデルに合致するよう予め、撹拌回転数を大きくしたり、反応管のＬ/Ｄ を大きくしたり工夫をしておく。

液相反応のように、実験データの解析から得られる反応速度定数は、解析に採用される混合モデルに直接的・間接的に依存し、唯一の絶対的な速度定数（真の速度定数）ではないことが多い。いわゆる総括の速度定数として求められている。反応速度定数はArrhenius式により定式化されることが多く、得られた頻度因子や活性化エネルギーの値は、用いた混合モデルが暗黙の内に含まれている。逆にいえば混合モデルが異なると、頻度因子や活性化エネルギーが異なる値となることはよく経験するが、できるだけ混合モデルに依存しない速度定数を求めることが望ましい。

実験上どうしても不完全混合モデル（後出）を適用しなければならないときには、実験装置（反応速度データを採取するための装置）そのものを利用して、滞留時間分布を測定し、混合モデルのパラメータを決める実験（実液ではなく、水などの擬似流体を用いる。モックアップテストという）を行うこともある。

装置内混合および混合モデルについては次節で詳しく述べるが、反応速度を解析する上で実験装置の混合モデルの選択は重要である。単純なプラグフロー反応器や完全混合槽反応器に近似できる試験装置であれば、特別な滞留時間分布測定実験をしなくてもよい。しかし、反応器構造が複雑な場合や不均一系反応の場合には、混合モデルを構築するための滞留時間分布測定実験を行うことがある。

先頭に戻る

物質移動・熱移動

気液、液々反応のような不均一系反応のとき、実験条件により相間の物質移動が律速段階になっていることがある。このような実験データを解析するときは、物質移動を考慮した反応器モデルを作る必要がある。物質移動が律速のとき、その物質移動係数が反応速度定数以外に未知数となる。既往の物質移動係数の相関式から求めた推算値を使うと、真の速度定数を求める際の誤差要因となることもあり、反応と物質移動の両方を精度良く解析できるよう実験計画を立てることが重要である。

不均一系反応、例えば気固・触媒反応や気液・ガス吸収反応のように、細孔内拡散や相間（界面）の物質移動を考慮しなければ反応速度が解析できないときもある。このような場合には、固体触媒反応の触媒有効係数2)、ガス吸収反応の反応係数14),16)を考慮し、速度定数を最適化する必要がある。反応速度定数以外に、物質移動係数などが未知のパラメータとなり、未知数の数が増えることになる。

熱移動については触媒充填管型反応器のように、反応熱や外部熱媒体との熱交換が支配的となる反応器では、その速度定数を決定するため温度分布を考慮した反応解析を実施しなければならないことがある。そして充填層と管壁との伝熱係数や流れ方向伝熱係数などのモデルパラメータが必要となり、これらを既存の相関式を利用して推算し、半径方向を含む円筒座標系の２次元で解くことになるが、計算機負荷が増大し、反応速度定数の最適化は煩雑なものとなる。また得られた速度定数は利用した相関式が正しいという前提の下での最適解であり、速度定数そのものがどこまで信頼できるか、の判断が難しい。

先頭に戻る

最適化の手法

真の反応速度を得るためには、プラグフローや完全混合といった混合モデルを含む、試験装置の反応器モデルを作成しなければならない。さらに、断熱反応のように熱収支をとる必要のあるもの、触媒が反応の進行とともに劣化するもの（たとえばコーキングや失活を考慮したモデル）、相間の移動現象が律速となるものなど、反応装置全体のモデル化を行い、モデルのパラメータや反応速度定数を同時に定式化・フィッティングする場合が多々存在する。軸方向拡散係数や物質移動係数など既存の相関式が利用できる場合には、未知パラメータとせず、既知とすることもある。

健全な実験データを用い、反応速度定数（Arrhenius式の頻度因子と活性化エネルギー）を求める最適化の方法について考える。

反応速度解析に当たり、反応モデルおよび混合モデルを考慮した反応器モデルを構築し、これを解く反応器シミュレータを開発することになる。いわゆる操作型の反応器シミュレータであり、入口のフィード条件（流量、組成）、反応条件（温度、圧力）、反応器サイズを与え、出口組成や反応成績を予測する。操作型反応器シミュレータは、スケールアップ用のシミュレータとしても利用できるよう、反応速度解析時に開発されることが多い。反応速度解析に用いるツールは、こうした操作型反応器シミュレータに、速度定数を最適化するための外部収束ループを上積みした構成となっている。従って、心臓部の反応器モデルを解くという部分は、反応速度解析用とスケールアップ用シミュレータとで共通して利用できる。

実験データの入口条件、反応条件、反応器サイズを与え、また反応速度定数を仮定し、反応器シミュレータにより出口の予測値を計算する。実験で得られた出口の実測値とこの予測値の差を最小とするよう、反応速度定数を修正することになる。最小二乗または最適化問題は、ある目的関数Obj が最小となる未知のパラメータを決定する問題をいう。パラメータ（独立変数）をx1、x2、･･･とすると、次のように表現できる。 \[ \begin{align*} Obj(x_1,x_2,\cdots,x_n) & \longrightarrow {Minimize} \tag{6} \\ Obj(x_1,x_2,\cdots,x_n) & = \sum_i \{ y_i - f_i(x) \}^2 \longrightarrow {Minimize} \tag{7} \end{align*} \] 最小二乗問題は、最適化問題に含まれる一つの問題であり、目的関数が、式(7)のように 観測値 yiと予測関数 f(x) で算出される予測値との差の２乗和（残差のノルム）を最小化するパラメータを求めようとする問題である。f(x) が線形の場合（例えば多項式）と非線型の場合とがある。Newton法やLevenberg-Marquardt法は非線型最小二乗法13)でよく使われる解法である。

一般の最適化問題に適用される最適化手法13)には、Powell法、Davidon-Fletcher- Powell法、シンプレックス法などがある。

先頭に戻る

流れ・混合の影響

反応器内流動特性

化学反応を伴うとき原料Ａと生成物Ｂの少なくとも２成分が存在し、これらの成分が流れを形成し、かつ反応場である反応器内部を流れる。ミクロな流体混合の程度により反応成績は影響を受けることが予想される。こうした反応器内部の混合挙動をできるだけ正確にまた厳密に構築しモデル化すると、反応器のスケールアップに伴う設計面のリスクを大幅に減じることができる。しかし、いくら厳密なモデルを構築しても、現有のインフラ環境やツールを使って解が得られるモデルでないと意味がなくモデルの簡素化がしばしば必要になる。

図５：基本的な混合モデル

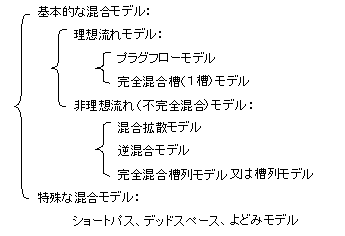
装置内の流れを表す基本的な混合モデルは、図５に示すように理想流れモデルと非理想流れ（不完全混合）モデルとに大別される。理想流れは更に両極端のプラグフローモデルと完全混合槽（１槽）モデルに分類され、一方不完全混合モデルは、混合拡散モデル、逆混合モデル、完全混合槽列モデルに分類される。装置内の混合特性を表す代表的な混合モデルを以下紹介するが、商業規模の反応器を理想流れモデルで近似する場合は極めて限定されており、非理想流れモデルや理想流れモデルを組み合わせたモデルで近似することが多い。

「流体の混合」を考えるとき、装置内の流れ（フローパターン）を知る必要がある。通常の反応器設計では装置内流れとして、移流項（Convectional Term:流れ速度に乗っかって物質が移動する効果）と、拡散項（Diffusional Term:分子拡散や乱流拡散により物質が移動する効果）の二つを考える。

図６：配管内の乱流模式図

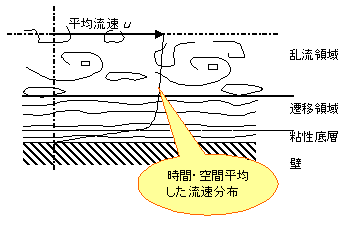
例えば、図６の配管内の流れによる混合を例にとると、マクロ的には流れ方向に平均流速ｕに乗っかって物質が移動する（移流項）。一方、局所的な濃度差をDriving Forceとする物質の分子拡散が存在する。流体の平均流速が大きく乱流領域になると、微小な乱流渦が数多く生成し、渦内部で局所的な濃度勾配ができ、渦内の分子拡散が起こる （前述の分子拡散と区別して、混合拡散、乱流拡散、渦拡散、Eddy Diffusionともいう）。通常の気相反応や低粘性流体の液相反応では、分子拡散よりも乱流による渦拡散が支配的であり、Eddy Diffusivity（混合拡散係数）が混合の程度を表す指標となる。

装置内の混合特性は一般に流れ方向の混合拡散係数Ezで整理されている。流れ方向（ｚ軸方向）の混合拡散係数Ezおよびこれを無次元化したペクレ(Peclet)数をレイノルズ数などの無次元数で表した相関式やチャートが数多く報告されている（後出）。

ペクレ数Peは一般に次式で定義される。 \[ \begin{align*} ペクレ数 {\rm Pe ~ [-]} = \frac {代表速度[m/s] \times 代表長さ[m]}{混合拡散係数[m^2/s]} \tag{8} \end{align*} \]

上式の分子に含まれる代表速度はガスや液の平均流速をとり、代表長さとして反応器の長さや直径、充填層のときは粒子径をとることもある。図書や文献でペクレ数というとき代表長さとして何を採用しているか、代表速度として空塔速度なのか充填層隙間の速度なのかに注意しないと、間違って推算することになる。ペクレ数の定義からわかるように、（8)式の分子は平均流速による移流項、分母は混合拡散による拡散項であり、移流項と拡散項の比となっている。ペクレ数が小さいと拡散項が大きく、拡散支配となる。混合拡散係数が無限大のとき、ペクレ数はゼロとなり、完全混合モデルとなる。逆に混合拡散係数がゼロのとき、ペクレ数は無限大となり、プラグフローとなる。

装置内混合特性を表す排出累積分布関数 F(t) およびこれを微分した滞留時間分布関数E(t) を知ることにより、装置の混合特性をモデル化し、予測することができる。実際には、こうした分布関数を利用して反応器設計を行うことは少なく、混合モデルを組み込んだ反応器シミュレータを介して、混合モデルのパラメータを直接入力し混合性能を予測したり、解析したりすることが多い。

先頭に戻る

理想流れモデル

理想的な混合特性をもつ二つの理想流れ反応器、すなわち拡散のないプラグフロー型（押出流れ、ピストン流れ、栓流ともいう）反応器と、瞬間的に混合される（拡散係数が無限大の）完全混合槽型反応器を考える。これら理想的な両極端の流れの過渡応答（パルス応答やステップ応答）を考える。

図７中段に示すパルス応答を考える。いま無次元化濃度ゼロの原料が連続的に図上段の2種類の反応器入口に供給されているとし、濃度無限大で時間幅ゼロ（デルタ関数、濃度を時間積分すると１となる）のトレーサーパルスを、時刻ゼロの瞬間に反応器入口に注入し、出口濃度の時間変化を観測する（フィード中にインクを垂らすイメージ）。中央の図に示すようにプラグフロー型反応器では、時間遅れθをもつ投入パルスと同一形状のパルスが観察される。一方完全混合槽型反応器では右端の図のように反応器に入った瞬間、均一混合されその後原料により薄められ、徐々に濃度ゼロに戻る経時変化が観察される。このときに観察される出口濃度の経時変化を滞留時間分布関数E(t) という。

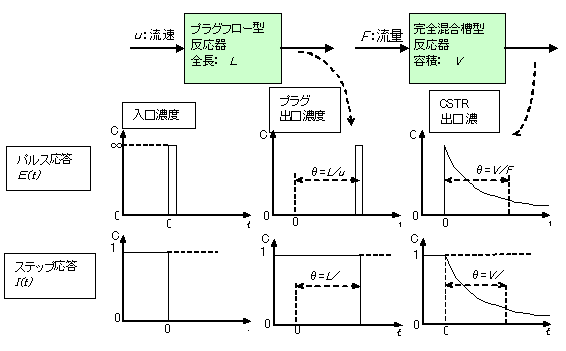
図７：パルス応答とステップ応答

一方、図７下段に示すステップ応答（原料の無次元化濃度を１からゼロに瞬間的に切り替えたとき）の出口濃度を観察すると、プラグフローでは時間遅れθを持つステップ状の濃度変化が観察される。一方完全混合槽では原料が入った瞬間に均一混合され、それが直ぐに出口に現われ、徐々に濃度ゼロに槽内が置き換わるという曲線となる。ステップ応答のときに観察される出口濃度の経時変化を年齢分布関数 I(t) という。

年齢分布関数 I(t) と滞留時間分布関数 E(t) との間には、平均滞留時間をθ（反応器容積を容積流量で除した値または長さを流速で除した値）とすると、次の関係がある。 \[ \begin{align*} E(t)=-\theta \frac{dI(t)}{dt} \tag{9} \end{align*} \]

先頭に戻る

プラグフローモデル（理想流れ）

図８：プラグフローモデル

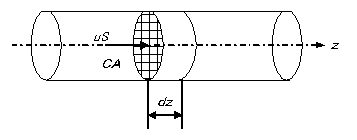
図８に示す管型の拡散のないプラグフロー型反応器で成分Ａの物質収支を考える。流れ方向をｚ軸、管断面積をＳ、平均流速をｕとし、微小区間dzで成分Ａの物質収支をとると、 \[ \begin{align*} \frac{\partial C_A}{\partial t} + u \frac {\partial C_A}{\partial z}=-r_A \tag{10} \end{align*} \]

となる。 定常状態では、(10)式は、 \[ \begin{align*} u \frac {\partial C_A}{\partial z}=-r_A \tag{11} \end{align*} \]

となる。ここで r A は反応による成分Ａの消費速度を示す。成分収支式(11)は、距離ｚについて１階の常微分方程式となり、境界条件を一つ与えれば解くことができる。通常ｚ = 0（反応器入口）で、成分濃度CA = CA0(原料の入口濃度)を与える。

（11)式の常微分方程式は、Runge-Kutta法などにより解くこともできるが、ここでは差分法により、解くことを考える。差分化（例えばオイラーの1次精度近似を採用）するとき、次の前進差分や後退差分9)により一階の微分項を近似する。 \[ \begin{align*} \frac {dC}{dz} & = \frac 1{\Delta z}(C_{j}-C_{j-1})+O(\Delta z) \tag{12a} \\ & = \frac 1{\Delta z}(C_{j+1}-C_{j})+O(\Delta z) \tag{12b} \\ \end{align*} \]

ここでCj はｊ番目の分割点の濃度を表している。O (Δz) は誤差項を示す。これを(11)式に代入することにより、左辺微分項が差分化され、分割点の数Nだけの連立非線型方程式系に変換される。差分化により得られるプラグフローモデルの基礎式は、後出の非理想流れの完全混合槽列モデルと全く同じ形となる。プラグフローモデルを差分法で解くとき、反応器を有限の数Nに等分割して解くが、その基礎式は槽列モデルと同じとなり、ただ分割数だけが異なることになる。したがって、反応器シミュレータを作成するとき、プラグフローを解くコードと槽列モデルを解くコードとを共用することができる。また槽列数Ｎとして１を許容できるようコードを作成すれば、次の完全混合槽１槽モデルも同じコードで解くことができる。

先頭に戻る

完全混合槽モデル（理想流れ）

図９：完全混合槽モデル

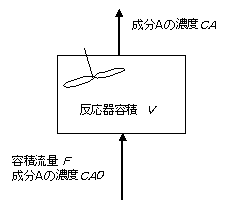
図９に示す完全混合槽（１槽）モデルの成分Ａの物質収支式を考える。完全混合槽モデルでは原料が反応器に入った瞬間に完全混合されると考え、槽内の濃度は出口濃度CAに等しいと考える。成分Ａの反応による消費速度をrAとし、非定常状態のときの成分収支式は、 \[ \begin{align*} V \frac {dC_A}{dt} & = FC_{A0}-FC_A-Vr_A \tag{13} \\ \end{align*} \]

となる。 定常状態では上式左辺がゼロとなり、成分の数だけの連立非線型方程式に帰着する。

定常状態の成分収支式(13)は、分割数N = 1としたプラグフローモデルの(11)式を差分化した式と同じ形となっている。シミュレーションのコード上、完全混合槽とプラグフローの差は分割数だけとなる。

先頭に戻る

非理想流れモデル

現実の反応器では先の二つの理想的な混合流れとなることは少なく、中間的な非理想流れ（不完全混合流れ）となることが多い。中間型流れの代表的なモデルとして、完全混合槽列モデル（単に槽列モデルともいう）、混合拡散モデル（Dispersion Model）、逆混合モデル（Back Mixing Model）がある。混合拡散モデルと逆混合モデルは数学的・解析的にほぼ同等であり、両者にあまり差はない。完全混合槽列モデルは、槽列数Ｎ を無限大にすればプラグフローモデルに帰着し、Ｎ =１とすれば完全混合槽（１槽）モデルに帰着する。Ｎを有限にとることにより中間の非理想流れモデルとなる。

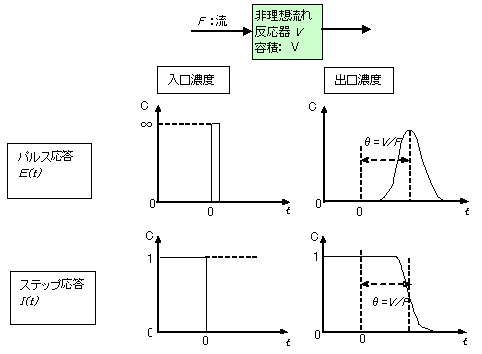
図１０：非理想流れ反応器の応答

非理想流れ反応器のパルス応答およびステップ応答を図１０に示す。パルス応答では、平均滞留時間θに相当した遅れ（プラグフローと同じ）と、投入パルスが前後に拡散し幅を持つ（完全混合槽と同じ）という２つの特徴を合わせ持ち、滞留時間分布関数E(t) は正規分布の形をとる。ステップ応答もプラグフローと完全混合の２つの特徴を持っている。

先頭に戻る

完全混合槽列モデル（非理想流れ）

図１１：完全混合槽列モデル

完全混合槽列モデルは、図１１に示すように、ひとつの反応器を、N個のセルに等分割し、それぞれのセルを完全混合槽（１槽）モデルとし、流れ方向の流れだけを考え、セルを直列につないだモデルである。Ｎ =１とすれば完全混合槽１槽モデルに、Ｎ = ∞とすればプラグフローモデルに帰着する。

第ｊ番目のセルを考え、成分収支式をとると、先の（13）式と同様に、 \[ \begin{align*} \frac VN \frac {dC_j}{dt}=FC_{j-1}-FC_j-\frac VN r_j \tag{14} \end{align*} \]

となる。ここで、Cjは第ｊセルの出口濃度である。完全混合槽列モデルの滞留時間分布関数 E(t) は次式で表される。ここでτは無次元化時間である。 \[ \begin{align*} E(t)= \frac {N^N}{(N-1)!} \tau ^{N-1} \exp (-N \tau) \tag{15} \end{align*} \]

先頭に戻る

混合拡散モデル（非理想流れ）

図１２：混合拡散モデル

図１３：Danckwertsの境界条件

混合拡散モデルは、図１２に示すように流れ方向をｚ 軸とし、微小区間dzで拡散項を考慮する。成分収支をとると次式が得られる。 \[ \begin{align*} \frac {\partial C}{\partial t} = E_z \frac {\partial^2 C}{\partial z^2} -u \frac{\partial C}{\partial z} - r \tag{16} \end{align*} \]

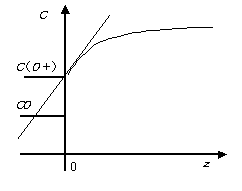
ここでEzは軸方向混合拡散係数である。定常状態では２階の常微分方程式となり、解くためには二つの境界条件を必要とする。通常、出口で拡散フラックス（dC/dz）がゼロ、入口ｚ＝0で、次のDanckwertsの入口境界条件2)を用いることが多い。 \[ \begin{align*} C_0=C(0+)- \frac{E_z}{u} \frac{dC(0+)}{dz} \tag{17} \end{align*} \]

ここでC0は原料の入口濃度、C (0+) は入口直後の濃度を示す（図１３参照）。

いま定常状態を仮定し、(16)式を流れ方向 (ｚ方向) に分割し差分化する。濃度の１階微分および２階微分として次の中心差分9)を採用し \[ \begin{align*} \frac{dC}{dz} & = \frac 1{2 \Delta z}(C_{j+1}-C_{j-1})+O(\Delta z^2) \tag{18} \\ \frac{d^2C}{dz^2} & = \frac 1{\Delta z^2}(C_{j+1}-2C_j+C_{j-1})+O(\Delta z^2) \tag{19} \\ \end{align*} \]

反応がないとした（16）式の右辺に代入し整理すると、 \[ \begin{align*} \biggl( \frac{E_z}{\Delta z^2}+ \frac{u}{2 \Delta z} \biggr) C_{j-1} + \biggl( - \frac{2E_z}{\Delta z^2} \biggr) C_{j} + \biggl( \frac{E_z}{\Delta z^2} - \frac{u}{2 \Delta z} \biggr) C_{j+1} = 0 \tag{20} \end{align*} \]

となる。すなわち第ｊ番目のセルの収支は、前後の一つのセルだけの影響を受ける。この式の形は後述の逆混合モデルとほぼ同等の形をしていることがわかる。また槽列モデルの(14)式に下流側の第j+1番目のセルの項を追加した形となっている。

混合拡散モデルの滞留時間分布関数 E(t) を、種々境界条件で解析的に求めた解が成書11),12)に報告されている。

先頭に戻る

逆混合モデル（非理想流れ）

図１４：逆混合モデル

図１４に、逆混合モデルの模式図を示す。反応器をＮ 個に等分し、入口セルと出口セルを除き、下流側セルから逆流βFがあるとするモデルである。逆流比βを次のように定義する（1/βを逆流比と定義することもある）。 \[ \begin{align*} \beta = \frac{逆方向流れの流量}{入口の正方向流れの流量} \tag{21} \end{align*} \]

いま、反応器の全容積をＶ、入口フィードの容積流量をＦ、成分Ａの反応消費速度rAとし、逆混合モデルで第ｊ番目のセルの成分収支を考える。第ｊ番目のセルの出口濃度をCA,jと表し、また原料の入口濃度をCＡ,0とすると、

ｊ=１のとき（入口のセル） \[ \begin{align*} \frac VN \frac{dC_{A,1}}{dt}=FC_{A,0}-(1+\beta)FC_{A,1}+ \beta FC_{A,2}-\frac VN r_{A,1} \tag{22a} \end{align*} \]

中央のセル (1 < j < N) では、 \[ \begin{align*} \frac VN \frac{dC_{A,j}}{dt}=(1+\beta)FC_{A,j-1}-(1+2\beta)FC_{A,j} + \beta FC_{A,j+1}-\frac VN r_{A,j} \tag{22b} \end{align*} \]

ｊ=N（出口セル）では、 \[ \begin{align*} \frac VN \frac{dC_{A,N}}{dt}=(1+\beta)FC_{A,N-1}-(1+\beta)FC_{A,N} -\frac VN r_{A,N} \tag{22c} \end{align*} \] となる。非定常問題のときは非線型の連立常微分方程式となり、Runge-Kutta-Gill法または差分法で解くことができる。また定常問題では、非線型連立方程式となり、Newton法などで解くことができる。逆混合モデルの基礎式(22)は、混合拡散モデルの基礎式(20)に類似し、前後のセルだけから影響を受け、その係数の定義が違うだけで式の形は同じである。以上のことから、槽列モデル、逆混合モデル、混合拡散モデルは差分化したときせいぜい前後３つのセルの項により表され、解析コード上の差異はそれほどなく、共通化することができる。

以上のように、代表的な３つの不完全混合モデルを紹介したが、これらモデルのパラメータの一覧を表２に示す。

表２：不完全混合モデルのパラメータ
完全混合槽列モデル 混合拡散モデル 逆混合モデル Remarks
パラメータの数 1 2 2
パラメータ N : 分割数 N : 分割数
Ez : 混合拡散係数		 N : 分割数
β: 逆流比

先頭に戻る

ショートパスとデッドゾーン

装置内混合に影響を与える特殊なモデルとして、図１５に示すショートパス、デッドゾーン、よどみ（Stagnant zone）がある。ショートパスの存在による混合不良、デッドゾーンによる反応容積の減少など、滞留時間分布に影響を及ぼし、更には反応成績に影響を与える。

図１５：滞留時間分布関数に影響を与える特殊モデル

これら特殊な混合モデルを用いた例がWesterterpの図書10)などに掲載・報告されている。

先頭に戻る

組み合わせモデル

現実の商業化スケールの反応器は、前述した混合モデルのどれか一つを使って表されることもあるが、複雑な構造を持つ反応器では、これら混合モデルを組み合わせたモデルとなる。

また、最小のコスト（反応容積ミニマム）で最大の利益（収率マックス）を生み出すため、物理的に反応器を２つ以上に分割することも工業的にはよく行われる。こうした分割した反応器を全体としてとらえると、混合モデルの組み合わせとなっている。また反応器の内部構造が多孔板や仕切板で複数の部屋に区切られているとき、１室（ユニット）をある混合モデルで近似し、これが直列に並んだものとしてとらえる方が取り扱いが楽になる。あるいは触媒や充填物のベッドが複数段積み重なっている反応器では、各ベッドをある混合モデルで近似し、このモデルが直列に並んだものとしてとらえる場合もある。

装置内の混合モデルを選択する上で、一般的に言えることは、

これら諸点を考慮し、適用すべき反応器の混合モデルを組み立てる。

先頭に戻る

反応器内滞留時間分布

反応器を非理想流れモデルで近似するとき、その非理想性の程度（ペクレ数）を知る必要がある。ペクレ数を知るには、滞留時間分布を知る必要があり、

などの方法がある。

(a)の流体解析手法による反応器内の流れ解析では、Ａ、Ｂの２流体の混合（反応を考慮しない）問題を解くことにより、解析格子点での流れ速度、濃度を絶対値として知ることができる。市販のCFDツールを利用し、直接、反応器の分布関数 E(t) や F(t) を計算することは難しい。CFD解析の結果として得られる濃度分布や速度分布を積分するなどして出口平均濃度を求める必要があり、滞留時間分布を得るには手間がかかる。また計算コストもかかる。

(b)のモックアップ試験による、滞留時間分布の測定例として、水や水飴を用いインクを注入し出口で吸光度測定し、混合パラメータを決めたり、特別にモックアップ装置を組まないで、試験装置を用いて原料中の不活性成分（反応しない溶媒など）の濃度を切替え、出口で濃度変化を観察し、滞留時間分布を測定する例もある。

複雑な構造で内部フローパターンが予測できない反応器であれば、小スケールの流動モックアップ試験装置を作り、水などを用い過渡応答試験を行うこともある。

(c)の公知の情報を利用する場合として、配管の混合拡散係数の相関式21)（図１６）、固定層や充填層の混合拡散係数の相関式21)（図１７）、気泡塔の相関式など、反応器のタイプにより多くの相関式6),8)が報告されている。これら公知の情報を活用することにより、モックアップ試験や流体解析を省略し、ペクレ数を知ることができる。

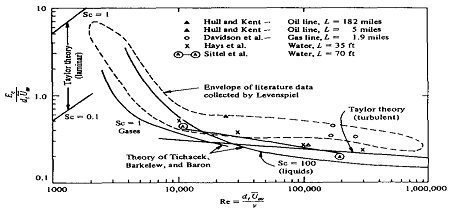
図１６：配管のペクレ数21)

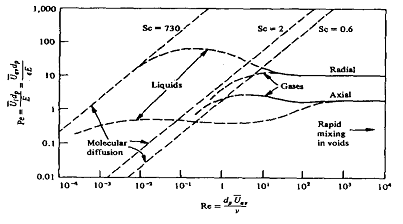
図１７：充填層のペクレ数21)

先頭に戻る

混合モデルの分散

非理想流れのとき、混合モデルの分散を比較することにより、モデルを変えたときのパラメータの値を推定することができる。例えば、混合拡散係数Ezがわかっているとき、これを槽列モデルに換算すると何槽に相当するのか、あるいは逆混合比βがわかっているとき槽列モデルでは何槽に相当するのか、など相互の換算ができる。

混合モデルの平均滞留時間θと滞留時間分布 E(t) の分散σ2を考える。分散とは簡単に言うと、滞留時間分布関数 E(t) （上に凸の山型の分布）のピークの半値幅（ピークの鋭さ）に相当する。分散が小さいということは、そのピークの半値幅が小さく、鋭いピークであることを示している。逆に分散が大きいと、ピークはブロードに広がった形になっていることを示している。

平均滞留時間をθとし、滞留時間分布の分散σ2は、 \[ \begin{align*} \sigma ^2 = \int_0^\infty (1-\theta)^2E(t)dt \tag{23} \end{align*} \]

で定義される。それぞれの混合モデルで導出される E(t) を上式に代入し、分散を導くことができる。西脇ら17) による導出結果を以下に示す。

完全混合槽列モデル： 槽数Ｎ とし次式で表される \[ \begin{align*} \sigma ^2 = \frac 1N \tag{24} \end{align*} \]

拡散モデル： 反応器の軸方向長さを代表長とするペクレ数Peとし、次式で表される \[ \begin{align*} \sigma ^2 = \frac{2}{{\rm Pe}^2} \biggl\{ {\rm Pe}-1+ \exp(-{\rm Pe}) \biggr\} \tag{25} \end{align*} \]

逆混合モデル： 分割数Ｎ、逆流比βを使い \[ \begin{align*} \sigma ^2 & = (1+\beta)^{1-N} \biggl[ \beta ^{N-1} + 2 \beta ^{N-2} \biggl( \frac{N-1}{N} \biggr) ^2 \\ & + \sum_{j}^N \beta^{N-j-1} (1+\beta) ^ {j-2} (j+1+2\beta) \biggl( \frac{N-j}{N} \biggr) ^2 \biggr] \tag{26} \end{align*} \]

で表される。これら式を用い分散を等置することにより、モデルのパラメータを相互に換算することができる。

Levenspiel7)は、拡散モデル（25）式と完全混合槽列モデル（24）式を等置し、次式を導出している。 \[ \begin{align*} \frac1N = \frac 2{\rm Pe} - \frac 2{{\rm Pe}^2} \biggl\{ 1 - \exp(-{\rm Pe}) \biggr\} \tag{27} \end{align*} \]

ただし、N が小さいとき誤差が大きい。

以上、装置内の流体混合について総括し、基本的な成分収支式、関連諸式を示した。基礎式は流れ方向（軸方向）だけを取り上げたが、半径方向の濃度分布や温度分布など三次元分布を考慮しなければならないときもあるが、ここに示した基本的な考えを拡張すれば、あらゆる反応器をモデル化することができる。こうした反応器モデルを前節で示した反応モデルとともに組み込んだ反応器シミュレータを作成し、シミュレーションすることで、反応器の挙動・成績を予測することができる。

工業的によく利用されるタイプの反応器モデル（例えば、撹拌槽型反応器、ガス吸収反応器、トリクルベッド型反応器、触媒充填管型反応器、気泡塔、通気撹拌型反応器、．．．．など）は、ほぼパターン化されており、数多くの成書5),6),8)や文献に紹介されており、手間をかけずに反応器をモデル化することができる。

先頭に戻る

演習問題

演習問題１：CSTR型とプラグフロー型反応器の容積比

図Ａ：CSTRとプラグの反応容積

連続流通型反応器で成分Aの出口転化率を \( x \equiv (C_{in}-C)/C_{in} \) とし、また反応速度がつぎのn次反応で表わされるとする。ここで、Cは成分Aのモル濃度を、kは速度定数を示す。 \[ \begin{align*} r=kC^n \tag{A.1} \end{align*} \]

完全混合槽型反応器(CSTR)とプラグフロー型反応器のそれぞれの必要な容積をVCSTRとVPLUGとし、これらの容積比VCSTR/VPLUGが、nにより次式で表わされることを証明せよ。

ｎ=1のとき \[ \begin{align*} \frac {V_{\rm CSTR}}{V_{\rm PLUG}} = \frac{ \displaystyle {\frac x{1-x}}}{ \ln \displaystyle {\frac 1{1-x}}} \tag{A.2} \end{align*} \]

ｎ≠1のとき \[ \begin{align*} \frac {V_{\rm CSTR}}{V_{\rm PLUG}} = \frac x{1-x} \biggl \{ \frac {n-1}{1-(1-x)^{n-1}} \biggr\} \tag{A.3} \end{align*} \]

【ヒント】

完全混合槽の物質収支(13)式から \[ \begin{align*} FC_{\rm in} - FC -V(-kC^n) & = 0 \tag{A.4} \\ C_{\rm in} - C -\theta (-kC^n) & = 0 \tag{A.5} \end{align*} \]

ここで、θ=V/F [hr]、Ｖは反応容積、Ｆは容積流量である。 \[ \begin{align*} \theta \equiv \frac VF = \frac {C_{\rm in}-C}{-r} \tag{A.6} \end{align*} \]

この式の右辺は図Ａのx方向の幅×ｙ方向高さの積になっており、面積aecdに相当する。上式に \( r=kC^n \) を代入し、転化率 \( x=1-C/C_{in} \)で表すと \[ \begin{align*} V_{\rm CSTR}=\frac {Fx}{kC_{\rm in}^{n-1}(1-x)^n} \tag{A.7} \end{align*} \]

となる。一方、プラグフローの物質収支(11)式から \[ \begin{align*} u \frac {dC}{dz} & = -r \tag{A.8} \\ \int_{C_{\rm in}}^C \frac 1{-r} dC & = \int_0^L \frac 1u dz = \frac Lu = \frac VF = \theta \tag{A.9} \end{align*} \]

ここで、ｕは流体の線速度（容積流量を流路断面積で割った値）、Ｌは反応器長さである。この式左辺の積分は図Ａの面積abcdに相当する。

上式に を代入・積分し、転化率 で表すと

n=1 のとき、 \[ \begin{align*} V_{\rm PLUG} & = \frac Fk \ln \frac 1{1-x} \tag{A.10} \end{align*} \]

n≠=1 のとき、 \[ \begin{align*} V_{\rm PLUG} & = \frac {F [1-(1-x)^{n-1}}{k(n-1)(1-x)^{n-1}C_{\rm in}^{n-1}} \tag{A.11} \end{align*} \]

となる。(A.7)、(A.10)、(A.11)式の比をとり、整理すると(A.2)、(A.3)式が得られる。（証明終）

先頭に戻る

演習問題２：

先頭に戻る

演習問題の解答

演習問題の解答は、ここ（未リンク）で取り扱っています。

先頭に戻る

Literature Cited

先頭に戻る