技術計算:物性・熱力学
現在工事中です。
ここでは化学工学分野で取り扱う物性と熱力学について解説します。「物性・熱力学」と大上段に構えると極めて範囲が広くなってしまいますので、 石油化学プロセスで、反応器設計・反応器シミュレーションに係わる部分をさらっと流す程度の内容とします。 詳細な議論は図書や文献を参照して下さい。
また、石油精製プロセスのようなLightからHeavyまでの連続成分を取り扱うのではなく、化学種として化学構造が解明され、特定できる成分を取り扱います。また 無機化学品ではなく有機化学品で、基本的にCarbon、Hydrogen、Oxygen(CHO)を含む物質を対象とします。
一方、ここで取り上げる物性や熱力学は、反応器シミュレーションに必要な物質収支や熱収支などの収支式に現れるもの、相間の物質移動や熱移動に係わるもの、および反応器設計に係わるもの、特に輸送物性などを中心に取り上げるつもりです。 また、物性・熱力学は取扱う範囲が広く、反応器の設計・シミュレーションに比較的よく現れるPVT物性、化学平衡、気液平衡の計算をトピックスとして取り上げました。 また必要に応じて、トピックスを追加するか、別ページで紹介することを考えています。
- 1. はじめに
- 2. 物性データベース
- 3. 熱力学関数の導出
- 3.1 NASAの熱力学関数
- 3.2 DIPPRの熱力学関数
- 3.3 混合物の熱力学関数
- 4. DIPPRによる物性推算方法(純物質)
- 5. 物性データの所在
- 6. 混合物の物性推算
- 6.1 物性推算コードの具体例
- 6.2 DLLによる物性推算ツール
- 6.3 反応器シミュレータの物性推算
- 6.4 反応器設計の物性推算
- 7. Topics 1: PVT物性の計算
- 8. Topics 2: 化学平衡の計算
- 9. Topics 3: 気液平衡の計算
- 10. 練習問題
- 11. Literature Cited
【注】数式表示にはMathJaxを利用しています。IE8以下では表示が遅くなる可能性があります。FireFox などIE8以外のブラウザを利用下さい。
はじめに
ここでは、化学工学および反応工学でよく使われる物性や熱力学関数について、その推算方法や利用の仕方について解説する。特に反応器設計や反応器シミュレーションに出現する物性値や熱力学関数について主に取り扱う。
反応器を設計・シミュレーションする上で出現する物性として、物質固有の物性定数(分子量、臨界定数など)がある。 また、物性値には、PVT物性(密度、比容)、熱物性、輸送物性などがある。 さらに、これら物性値には、純成分の物性値と混合物となったときの物性値がある。 さらに、純成分および混合物の相(気液固)によっても物性値の値が変わり、推算方法も変わってくる。
混合物の場合にはさらに2成分パラメータが実験データをフィッティングするとき導入されることが多いが、2成分パラメータを推算することは現時点ではほとんど 不可能であり、通常は理想的な混合則を用いることが多い。
一方、熱力学関数は、代表的には理想気体状態での定圧比熱を温度の多項式近似として表現し、これを積分することにより エンタルピー、エントロピー、フガシティー、さらには自由エネルギーなどを熱力学的関係を用いて導出することができる。 積分するに当たり、積分定数を必要とするが、通常標準状態での値が用いられる。 これら熱力学関数が与えられると、反応熱や化学平衡定数などの推算が可能となる。
反応器設計やシミュレーションを含めて反応工学の分野では、次の物性値がよく利用される。
- 1) 熱力学関数:エンタルピー、エントロピー、自由エネルギー、フガシティー、反応熱、化学平衡定数
- 2) 物性定数:分子量、臨界定数、沸点、融点、偏芯係数、双極子モーメント、Lenard-Jonesパラメータなど
- 3) PVT物性:密度、蒸気圧、体・線膨張係数、圧縮率、Joule-Thomson係数、ビリアル係数
- 4) 熱物性:比熱、相変化に伴う潜熱など
- 5) 輸送物性:粘度、熱伝導度、拡散係数、表面張力など
- 6) 混合則(Mixing Rule):物性値ではないけれど必要なアイテム
- 7) 混合物:気液平衡、液液平衡、ヘンリー定数、溶解度など
物性データベース
前述の物性値は、純物質の物性値の場合もあれば、複数の物質からなる混合物の物性値の場合もあり、ともに実測値や推算するための定数、推算方法を必要とする。 また物質の相ごとに違う値をもつ。
反応器設計や反応器シミュレーションでは、純物質のパラメータを入力しておき、その温度の純物質の物性値を計算し、最適な混合則(Mixing Rule)を適用し混合物の物性値を推算できる必要がある。 また物質が高温・高圧下にあるときはそれなりの補正を必要とする場合がある。
反応器設計やシミュレーションで、物性を推算するための物性データベースは必要不可欠なものであり、市販のプロセスシミュレータや各種の データベースから利用できる。
有料ではあるが、データベースのうち、 AIChEのDesign Institute for Physical Properties(DIPPR)では次の物性値の温度依存性を式で表し、その係数を物質ごとにテーブル化している。 もちろん一般的な物性定数(臨界定数、沸点、融点など)もテーブル化している。DIPPRにより推算可能な物性の一覧を表1に示す。
| No. | 物性値 |
|---|---|
| 1 | 固相密度 |
| 2 | 液相密度 |
| 3 | 蒸気圧 |
| 4 | 蒸発潜熱 |
| 5 | 固相定圧比熱 |
| 6 | 液相定圧比熱 |
| 7 | 理想気体の定圧比熱 |
| 8 | 第2ビリアル係数 |
| 9 | 液相粘度 |
| 10 | 気相粘度 |
| 11 | 液相熱伝導度 |
| 12 | 気相熱伝導度 |
| 13 | 表面張力 |
こうした物性値の推算は、市販のAspenやPro/2といったプロセス・シミュレータでも実施できる。しかしながら、新たに化学品の製造プロセスを開発したり、改良する場合には 独自の、信頼性のある物性データベースを構築する必要があったり、現に構築し、有している場合がある。こうしたときには、信頼性のある独自の物性定数を利用して化学工学計算(反応器設計・シミュレーション)を実施することが望ましい。 市販のシミュレータに独自の物性データベースを組み込むことは可能ではある。 しかし、こうした市販のシミュレータでは、反応器を設計・シミュレーションする場合には単位操作としての「反応器」の機能が極めて限定的で、制限があることが多い。 すなわち、完全混合槽型反応器やプラグフロー型反応器などに限定されていたり、 理想的なGibbs反応器のような平衡反応器であるなど、 少し高度な反応器モデル(物理的な混合モデル)が用意されておらず、市販シミュレータに組み込もうとすると多大な労力を必要とする場合が多い。
また反応速度式を市販のシミュレータに組み込むとき、反応速度式がArrhenius型で簡単なものであれば容易に組み込むことができるが、触媒サイトへの吸着・脱着過程が あったり、複合反応や競争反応など複雑な速度式を組み込むとなるとかなり面倒な作業となる。
こうした多大な労力を費やすならば、独自のシミュレーション環境を構築した方が次の点で望ましい。 すなわち、 計算速度の向上、メンテナンス性の向上が期待でき、改良・改善が容易となる、将来の移植性が保証される、コードのブラックボックス化が妨げられすべて既知でオープンな環境でシミュレータを構築できるなどメリットが多い。
独自のシミュレーション環境を整えるとき、もっとも簡便な物性推算手法は、DIPPRの物性定数を組み込むことである。また同時に定圧比熱の推算式をあらかじめ積分し、エントロピー、エンタルピーを定式化しておくことで 熱力学関数を推算することができる。
DIPPRで取り扱える物性は、反応器設計や反応器シミュレーションで必要とする多くの部分をカバーしており、使い勝手がよい。
熱力学関数の導出
反応器シミュレーションで熱収支を取るとき、反応器入口および出口のエンタルピーを用いる場合、エンタルピーに標準生成熱が考慮されているなら反応熱も含めた計算がなされる。しかし比熱を用いて熱収支をとるときには反応熱を別途考える必要がある。 ここでは熱力学関数として反応工学で頻繁に現れるエンタルピー\( H \) 、エントロピー \( S \) およびGibbsの自由エネルギー \( G \) の計算方法を解説する。これら熱力学関数は化学平衡を考えるとき化学平衡定数の計算にも利用される。
純物質の定圧のときのエンタルピー変化およびエントロピー変化は、定圧モル比熱を積分して次式で計算される。 \[ \begin{align*} H_{}-H_{T_0} & = \int_{T_0}^{T} C_pdT \tag{1} \\ S_{}-S_{T_0} & = \int_{T_0}^{T} \frac {C_p}{T} dT \tag{2} \\ \end{align*} \]
ここで \( T_0 \) は基準となる温度を示す。通常 298.15K が採用され、そのときのエンタルピー \( H_{T0} \) として25℃における標準生成熱を採用することが多い。 エントロピーも \( S_{T0} \) として25℃の標準エントロピーを採用することが多い。標準生成熱を採用することにより、反応熱や自由エネルギーの変化などの計算が可能となる。
熱力学関数\( H,S \) などは、定圧モル比熱の式の形が与えられると、(1)式および(2)式を積分することにより得ることができる。 定圧比熱の式には、典型的には多項式によるNASA(National Aeronautics and Space Administration)の形式や、特殊な形ではあるが、DIPPRの式で与えられることがある。 また分子のグループ寄与法によるJobackの方法やBensonの方法でも温度の多項式の係数を推算することがでる。
NASAの熱力学関数
ここでは温度多項式を用いたNASAの定圧比熱式から熱力学関数を導出する3)。Jobackの方法やBensonの方法による温度多項式にも当てはまる。まず、 NASAの7-term polynomialsによる熱力学関数 \( C_p \) は(3)式で与えられる。これを(1)、(2)式に代入すると、エンタルピー、エントロピー\( H,S \) が、またGibbs自由エネルギー \( G \) の定義式から、関数形は(4)~(6)式で表される。 パラメータ \( a_1,\cdots,a_7 \) は多くの純物質に対し報告されている2)。 \[ \begin{align*} \frac {C_p^\circ}{R} & = a_1 + a_2T + a_3T^2 + a_4T^3 + a_5T^4 \tag{3} \\ \frac {H^\circ}{RT} & = a_1 + \frac {a_2T}{2} + \frac{a_3T^2}{3} + \frac {a_4T^3}{4} + \frac {a_5T^4}{5} + \frac{a_6}{T} \tag{4} \\ \frac {S^\circ}{R} & = a_1 \ln T + a_2T + \frac{a_3T^2}{2} + \frac {a_4T^3}{3} + \frac {a_5T^4}{4} + a_7 \tag{5} \\ \frac {G^\circ}{RT} & = \frac {H^\circ}{RT} + \frac {S^\circ}{R} \tag{6} \\ \end{align*} \]
同様にBurcat.THRデータベース3,4)に、 NASAの9-term polynomialsによる熱力学関数 \( C_p,H,S \) の関数形は次式で表され、パラメータ \( a_1,\cdots,a_9 \) は多くの純物質に対し報告されている。 \[ \begin{align*} \frac {C_p^\circ}{R} & = \frac {a_1}{T^2} + \frac {a_2}{T} + a_3+a_4T+a_5T^2 + a_6T^3 + a_7T^4 \tag{7} \\ \frac {H^\circ}{RT} & = - \frac {a_1}{T^2} + \frac {a_2 \ln T}{T} + a_3 + \frac {a_4T}{2} + \frac {a_5T^2}{3} + \frac {a_6T^3}{4} + \frac {a_7T^4}{5} + \frac{a_8}{T} \tag{8} \\ \frac {S^\circ}{R} & = - \frac {a_1}{2T^2} -\frac {a_2}{T} + a_3 \ln T + a_4T + \frac{a_5T^2}{2} + \frac {a_6T^3}{3} + \frac {a_7T^4}{4} + a_9 \tag{9} \\ \end{align*} \]
なお、Gibbsの自由エネルギーは(6)式と同じ形となる。
DIPPRの熱力学関数
一方、DIPPRによる純物質のガスの定圧モル比熱の推算式は(10)式で与えられる。液比熱は温度の多項式が用いられ、積分形はNASA式とほぼ同等となる。 理想気体のときの定圧比熱 \( C_p \) の式を積分してエンタルピー、エントロピーを定圧比熱の係数と積分定数 \( H_0,S_0 \) を用い計算できる。 DIPPRの比熱の式は、双曲線関数を用いており、NASAの多項式などと比べ特徴的である。 \[ \begin{align*} C_p & =A+B \biggl[ \biggl( \frac CT \biggr) \biggl/ \sinh \biggl( \frac CT \biggr) \biggr]^2 +D \biggl[ \biggl( \frac ET \biggr) \biggl/ \cosh \biggl( \frac ET \biggr) \biggr]^2 \tag{10} \\ H-H_0 & = AT + BC \coth \biggl( \frac CT \biggr) - DE \tanh \biggl( \frac ET \biggr) \tag{11} \\ S-S_0 & = A \ln T + B \biggl[ \frac CT \coth \biggl( \frac CT \biggr) - \ln \biggl| \sinh \biggl( \frac CT \biggr) \biggl| \biggr] \\ & - D \biggl[ \frac ET \tanh \biggl( \frac ET \biggr) - \ln \cosh \biggl( \frac ET \biggr) \biggr] \tag{12} \\ G & = H + TS \tag{13} \end{align*} \]
混合物の熱力学関数
NASAの多項式あるいはDIPPRの式により純物質の定圧比熱の係数が報告されている。 従って温度が与えられると \( C_p,H,S,G \) をその物質に対して計算することができる。 通常これら熱力学関数値は、モル当たりの熱量で算出される。混合物の場合に、混合による潜熱(混合熱など)の変化が生じなければ、モル分率 \( x_i ~ (i=1,N) \) による加成性により、混合物の熱力学関数値を算出することができる。 \[ \begin{align*} C_{p,{\rm mix}} & = \sum _{i=1}^{N} x_i C_{p,i} \tag{14} \\ H_{\rm mix} & = \sum _{i=1}^{N} x_i H_{i} \tag{15} \\ S_{\rm mix} & = \sum _{i=1}^{N} x_i S_{i} \tag{16} \\ G_{\rm mix} & = \sum _{i=1}^{N} x_i G_{i} \tag{17} \\ \end{align*} \]
これら熱力学関数の計算および後述の物性推算の計算をコード化し、DLL(Dynamic Linkage Library)化することにより、MS-Excelなどから呼び出し、物性値等をExcelのシート上で簡単に推算することが可能となる。 FortranコードをDLL化する方法については、こちら計算機・VBAとDLLとの連携を参照されたい。
DIPPRによる物性推算方法(純物質)
PVT物性、輸送物性など上述の熱力学関数以外の物性推算方法については、Prausnitzら1)の成書に詳しく記載されている。 これら成書は、物性定数の改良・修正などのメンテナンスがなされず、間違った、信頼性の低い値を推算する可能性がある。 しかしDIPPRでは、実験データとの比較、メンテナンスが常時行われており、信頼性が日々高められている。多種類の、しかもまとまった信頼性のある物性値を提供しているという点でDIPPRは、利用価値が高いといえる。
純物質の物性推算
DIPPRでは、先の表1に示す純物質の物性値が推算できる。たとえば純物質の第2ビリアル係数や粘度 \( \mu \) 、熱伝導度\( \lambda \) を次式で表し、 成分毎に係数が与えられていて、任意の温度の物性値を推算することができる。 また固相、気相、液相ごとにその式番号と係数がデータベース化(テーブル化)されている。
\[ \begin{align*} 第2ビリアル係数 & = A + \frac {B}{T} + \frac {C}{T^3} + \frac {D}{T^8} + \frac {E}{T^9} \tag{18} \\ \mu & = \frac {AT^B}{\displaystyle {1+\frac CT + \frac D{T^2}} } \tag{19} \\ \lambda & = \frac {AT^B}{\displaystyle {1+\frac CT + \frac D{T^2}} } \tag{20} \\ \end{align*} \]
DIPPRによる式番号と式の形を図1に示す。反応器設計・解析および反応器シミュレーションに現れるほとんどすべての物性推算をDIPPRにより行うことが可能であり、 DIPPRのデータベースを利用することを本ウェブサイトでは前提としている。
DIPPRでは、理想気体としての気相比熱が図1の(107)式として定義され、係数\( A,B,C,D,E \) が与えられる。 (11)~(13)式の、積分定数に相当する\( H_0, S_0 \) を 標準状態のエンタルピーやエントロピー値(これらもDIPPRで与えられている)から決められる。 従って、気相のエンタルピーやエントロピーなどの理想気体状態の熱力学関数は、温度のみの関数となる。
反応器が気液二相のときには、気液のエンタルピー差が沸点で蒸発潜熱となるように、液相エンタルピーの積分定数を調節しておく。 これにより、気液のエンタルピー差を求めたとき蒸発潜熱となり、熱収支も簡単にとることができる。
高圧の物性推算ほか
DIPPRで与えられる物性の係数はほとんどが低圧の、理想気体状態の物性値を推算できるが、気体の物性で高圧の場合には圧力依存性を別途考慮する必要がある。 圧力依存性についてはDIPPRでは与えられていないので、ユーザーが補正ルーチンを組み込む必要がある。
表1になく、反応器設計や反応器シミュレーションで比較的現れる物性として、気相および液相の拡散係数がある。拡散係数は2成分パラメータではあるが、 混合物中の成分の拡散係数を必要とする場合がある。拡散係数の推算方法は、Prausnitzらの図書1)に詳しい。
DIPPRの物性定数に載っていないものに、Lennard-Jonesパラメータの\( \sigma,\varepsilon/k \) があり、これもPrausnitzらの図書で推算しておき、コードに埋め込む必要がある。 これらは衝突積分を用いる粘度、熱伝導度、拡散係数などの輸送物性推算に必要となる。
物性データの所在
純物質の物性値を調べようとするとき、多くのデータベースが利用できる。主な図書、機関、ネットなどの環境を次に示す。
- 1) 物性値の所在(図書):
Internatinal Critical Table (古い実測データ多数)
化学工学協会編:物性定数、丸善
JANAF:"Thermochemical Tables",NBS (ガス成分の熱力学関数)
Perry's Chemical Engineer's Handbook
化学工学便覧
化学便覧 (標準生成熱、顕熱などデータあり)
- 2) DIPPR (有料)
基本的な物性(気固液)が揃っている。 - 3) NISTのWeb Database(無料)
ラジカル、気相成分、液相データ多数 - 4) NASAのDatabase:(Burcat et al.)
気相成分の熱力学データ
これらデータベースで該当する成分がないとき、分子構造から推算する方法がある。代表的なものとして、 Jobackの方法6)、Bensonの方法13)がある。
Jobackの方法では、標準沸点、融点、臨界定数、標準生成熱、標準自由エネルギー、理想気体の比熱の温度依存性、蒸発潜熱、溶融熱、液粘度の推算が可能である。 また、Prausnitzらの図書1)では、Constantinou & Gani法(CG法)7,8)、Domalskiらの方法9,10,11)も記載している。
Bensonの方法は、理想気体のガス比熱の温度依存性、標準生成熱、標準エントロピーなど分子構造から推算可能としている。
なお上述の図書などには2成分系のデータ等が含まれているものもあるが、 気液平衡、液液平衡をはじめとする2成分系、多成分系の平衡データは、GmehlingらのDECHEMAのデータシリーズ(図書)がある。Azeotropic Dataも成書12)にある。 気液平衡データなど反応器シミュレーションに利用する機会は少なく、気液間に物質移動が発生するような反応器では必要となる。
混合物の物性推算
化学プロセスの設計において、物質の物性は必要不可避な基本的なデータです。組成、温度、圧力により物性がどのように変化するのかを正確に予測・推算することが必要となります。 ここでは、プロセスエンジニアが、PRO/2やAspenといった市販のシミュレータに依存せず、手軽に物性計算・物性推算ができるような方法について紹介する。
化学製造業で働くプロセスエンジニアが担当する化学製造プロセスでは、膨大な数の物質を取り扱うことはまずない。 多くて数十程度、少ないときは数個程度です。 特に反応器設計や反応器シミュレーションでは原料と製品となる物質、中間反応があれば中間製品、副反応があれば副生物質を考慮すればよく、これら化学物質は せいぜい10個とか20個程度で済む。
化学プロセスでストリームという配管内の流体(温度、圧力、組成が違う)単位で装置設計を行う。ストリームはほとんどが混合物であり、物性も混合物の物性値として推算する必要がある。 DIPPRでは純物質の物性値を取り扱っており、適当な混合則(Mixing Rule)を適用し、混合物の物性を推算しなければならない。
混合則については、Prausnitzらの成書1)に詳しく、ここでは詳述するつもりはなく、別ページで改めて紹介したい。
物性推算コードの具体例
筆者が経験した多くの化学製造プロセスのシミュレーションや設計検討では、取り扱う成分の、DIPPRのテーブルの係数をリストアップし、MS-Excelのシート上にテーブルを作成します。 作成したMS-Excelのシートを、そのままTXT出力し、TXTファイルに変換します。そしてこのTXTファイルを テキストエディタで編集し、Fortranコードに変換し、BLOCK DATA化します。 こうすることにより、Fortranでいう COMMON エリアに係数をセットすることになります。 リスト1に作成したBLOCK DATAルーチンのFortranコードの例を示します。
次に、純物質の物性値を推算するサブルーチン、混合物の物性値を推算するサブルーチンを作成する。 これらサブルーチンを新たに開発することはなく、過去のコードを見直し・追加する程度の簡単な作業を実施し、 物性ルーチンを完成させる。
リスト2は、圧力PB、温度TK、フラグINDを引数として混合物の物性を計算する関数ルーチンの例です。 組成の配列ZINは、COMMON変数経由、高圧補正の有無フラグISWHPもCOMMON変数経由で与えています。 Fortranコード上でこれらCOMMON変数に組成をセットし、温度・圧力を引数として関数Y_PHYPを呼び出すことにより、フラグで指定 した混合物の物性値が計算され、返り値として戻される。
フラグINDは、リスト2で一部示したように、どの相のどんな物性値を推算するのかを区別する整数になります。 Y_PHYPルーチンでは、まず純物質の物性値を計算し、それから適切な混合則を使い混合物の物性を計算し、その結果を返します。
なお純物質の物性値が必要なときは、その成分以外の組成をゼロとし、混合物の物性計算を行えば得ることもできる。
こうした一連の作業はルーティン化されていて、DIPPR定数のExcelシートへの書き写しと、計算された物性値のデバッグがメインワークとなる。
DLLによる物性推算ツール
反応器を設計するとき、あるいは他の機器の化学工学計算をするとき、ほとんどのエンジニアはMS-Excelのワークシートを 日常的に利用している。このとき、例えば Reynolds数やPrandtl数を計算するとき、物性値が必要になる。 混合物の物性値は、組成、温度、圧力の関数であるので、これらの値を引数としてExcelのユーザー定義関数を呼び出して計算できれば、 効率的な作業が実現できる。
リスト2に示したようにDIPPR定数をFortranに落とし込み、物性推算ルーチンができているので、これをDLL化し、 VBA(Visual Basic Application)を経由し、MS-Excelから利用することができる。 物性ルーチンは、反応器シミュレータと同じルーチンを利用することができる。
そして、MS-Excelから利用できるように、DLLとExcelのインターフェイス部分をVBAで作成すればよい。
リスト3は、MS-Excelのワークブックのモジュールに記述するVBAの一部を示す。 DLLライブラリのY_PHYS関数は、物性フラグIND、圧力PB、温度TK、組成を格納する構造体COMP、などを引数とし 物性を計算し、結果を戻す。Y_PHYSルーチンの中で、組成をZINにコピーし、先のY_PHYPルーチンを呼び出している。
VBA(ExcelのBasic言語)の制限として、ユーザー関数の引数の最大値は29個であり、フラグ、圧力、温度、組成など 引数の総数を29個以下に抑える必要があり、VBAの構造体とFortranの構造体とはReference渡しでやり取りできるので、 組成は構造体経由で受け渡しをするように組んでいる。
VBAで定義したY_PHYPMX関数を用いることで、MS-Excel上で物性値入りの物質収支表(material balance sheet)を作成することも可能となる。 プロセスフローのストリームをワークシートの1列に対応させ、各成分の組成、全流量、圧力、温度をセルに記述し、これらを引数とする物性計算のユーザー関数をセルに記述することにより、 1列をひとつのストリームに対応させ、横(行)方向に、ストリームを並べ、物性計算セルを横方向にコピーすることにより物質収支表が出来上がる。
図2にMS-Excelで作成した物質収支表のサンプルを示す。
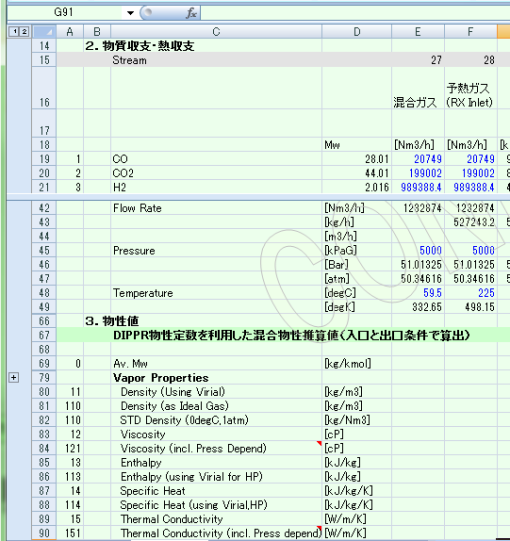
図2:Excel上の物性値計算の例
反応器シミュレータの物性推算
反応器シミュレータ(反応器内部を流れ方向に分割し、物質収支や熱収支をシミュレートする)で必要とする混合物の物性は、密度、輸送物性(粘度、熱伝導度)、比熱、熱力学関数などである。 反応熱や化学平衡定数は、反応のエンタルピー変化、自由エネルギー変化から計算できる。 これら物性推算は、DIPPRの定数をベースに作った先のルーチンを呼び出すことにより計算できる。
DIPPRベースの物性定数で、物性ルーチンを組むことにより、DLLとしても利用でき、また反応器シミュレータにも利用できる。 コード開発の工数節約にもなるし、コードの再利用が可能となり、DIPPR定数以外は同じコードを使い回すことでバグが減り、信頼性向上にもつながる。
反応器設計の物性推算
反応器の設計計算は、多くの場合、無次元化されていて無次元数を計算し、化学工学パラメータを推算することを行う。 たとえば、撹拌槽を設計するとき、内部流体の密度、粘度、熱伝導度などの情報から、撹拌回転数、撹拌動力、ジャケットやコイルの伝熱係数を推算する。 これら物性値をMS-Excelのシート上で、組成・温度・圧力を引数とし、上のDLL化した物性ライブラリを呼び出すことにより、物性値を取得できる。 そして撹拌回転数を決めて、撹拌動力や伝熱係数を過去の相関式を用いてMS-Excelワークシート上で計算し、撹拌槽を設計する。
物性ルーチン以外に撹拌動力や伝熱係数の既存の相関式などをDLL化すれば、こうした一連の作業をひとつのExcelシート上で実行できる。 MS-Excel上でケーススタディやゴールシークといった最適化計算に利用できる。
Re-Npチャートを始め、伝熱係数の相関式、などなど化学工学で現れる膨大な単位操作に係わる相関式を整理し集めた、R&Dツールについてはここ(未リンク)を参照されたい。
Topics 1:PVT物性の計算
PVT物性の計算とは、温度・圧力・容積のうち2つを与え、残る1つの変数を計算することである。 DIPPRの物性計算では第2Virial係数を推算し、気相容積を計算できる。気相容積の計算には対応状態原理(CSP:Corresponding State Principle)を 利用し、チャート(z線図)で計算するものがある。また状態方程式(Equations of State)を利用するものがある。
ここでは状態方程式によるPVT物性の計算について解説する。状態方程式を用いることにより気相のみならず液相のPVT物性、熱力学の関係から導出される各種状態量まで推算することができる。
たとえば、水の状態方程式はスチームテーブルにも記載されているように複雑ではあるが計算コードが公開されている。熱力学の関係を用い、気液の比熱、エンタルピー、エントロピー、自由エネルギーなどの状態量を温度と圧力の関数として計算することができる。
反応器設計やシミュレーションでは複雑な状態方程式よりも単純で精度のある3次の状態方程式を利用することを考え、以下紹介する。
3次の状態方程式
臨界点以下の領域では、van der Waalsは、気相および液相の容積が求められる、容積(または密度)について3次の状態方程式(cubic EOS)を提案した。 その後、気液密度を精度良く、また気液平衡を精度良く表すことができる3次の状態方程式、RK式、SRK式、PR式などが提案され、 市販のプロセスシミュレータに装備され、プロセス・エンジニアリング業務に広範に用いられている。これら著名な状態方程式を反応器設計や反応器シミュレーションでも利用できるように、コード開発 を行うことを考える。
3次の状態方程式は、数学的には3次の代数方程式となっており、カルダノの方法により解析的に解くことが可能である。
PVT物性計算で、もっとも単純な理想気体の法則がある。 低圧の場合には理想気体の法則による計算値で十分な場合もあるが、より精度の高い状態方程式を適用するとき、第1次近似値(収束計算の初期値)として理想気体則を使うことがある。 \[ \begin{align*} PV = nRT \tag{21} \end{align*} \]
理想気体の法則に比べ、より実在気体に合うように、分子を剛体球とみなし、分子間の引力を仮定して導出された、次の van der Waalsの状態方程式(22)式がある。容積\( V \) に対して3次式となっており、圧力・温度を与えるとCardano法により解析的に解くことができる。 条件により、3つの実根か1つの実根と2つの虚根の2通りが求められる。 \[ \begin{align*} P & = \frac {RT}{V_m-b} - \frac {a}{V_m^2} \tag{22} \\ \end{align*} \]
同様に、van der Waals型の 3次の状態方程式として、以下のRedlich-Kwong(RK)式14)がある。 \[ \begin{align*} P & = \frac {RT}{V_m-b} - \frac {a}{T^{1/2}V_m(V_m+b)} \tag{23} \\ \end{align*} \]
同様に、Soave-Redlich-Kwong(SRK)式15)がある。 \[ \left. \eqalign{ \begin{align*} P & = \frac {RT}{V_m-b} - \frac {a \alpha }{V_m(V_m+b)} \\ \alpha & = \Bigl[ 1+m \Bigl\{ 1 - \Bigl( \frac {T}{T_c} \Bigr) ^{0.5} \Bigr\} \Bigr] ^ 2 \\ m & = 0.480+1.574 \omega -0.176 \omega ^2 \\ \end{align*} } \right\} \tag{24} \]
また、同様に、Peng-Robinson(PR)式16)がある。 \[ \left. \eqalign{ \begin{align*} P & = \frac {RT}{V_m-b} - \frac {a \alpha }{V_m(V_m+b)+b(V_m-b)} \\ \alpha & = \Bigl[1+m \Bigl\{ 1 - \Bigl( \frac {T}{T_c} \Bigr) ^ {0.5} \Bigr\} \Bigr]^2 \\ m & = 0.37464+1.54226 \omega -0.26992 \omega ^2 \\ \end{align*} } \right\} \tag{25} \]
これらはいずれも温度・圧力が既知のとき、容積\( V \) について3次式となり解析的に解ける。 これらvan der Waals型の3次の状態方程式は、低圧以外の中・高圧のPVT挙動の推算に用いられる。 状態方程式からフガシティー係数を変形し、導出できることから、高圧の気液平衡を求める際にも適用でき、プロセス設計面で適用範囲は非常に広い。
Topics 2:化学平衡の計算
ギブス自由エネルギーから化学平衡定数を計算することができる。そして化学平衡組成はGibbs自由エネルギーを最小にするように最適化することで得ることができます。 演習問題として、数値解析:非線形方程式で取り扱っています。
Lagrange乗数を用いたGibbs自由エネルギーの最小化法L2982,L2985)により、初期組成をもつ混合気体の、圧力一定のもとでの化学平衡組成を求めることができる。 いま、平衡反応式がわかっており、\( n \) 成分系の混合気体を考える。初期組成が与えられ、温度・圧力がそれぞれ \( T,P \) とするときの化学平衡組成を求める。
ゼロでないLagrange乗数\( \lambda_i \) を導入する。(26)式は、平衡状態でGibbs自由エネルギーが最小となることから導出される。 (27)式は、元素バランスの式、(28)式は化学ポテンシャルの定義であるL2982)。 \[ \begin{align*} \mu_j + \sum_{i=1}^l {\lambda_i \alpha_{ij} } & =0, ~~~ (j=1,n) \tag{26} \\ \sum_{j=1}^n {\alpha_{ij} n_j } - b_j^0 & =0, ~~~ (i=1,l\ ) \tag{27} \\ \mu_j =\mu_j^0+RT\ln p_j & = \mu_j^0 + RT \ln {\biggl( \frac{n_j}{\Sigma n_i} \biggr) } + RT \ln P \tag{28} \\ \end{align*} \]
ここで、
\( \mu_j,(j=1,n) \) は、\( T,P \) 一定のときの成分\( j \) の化学ポテンシャル。 \( n \)は化学種の数
\( \mu_j^0 \) は、\( T,P \) 一定のときの1atmにおける理想気体の化学ポテンシャル[J/mol](純成分 \( j \) の自由エネルギー \( G_j^0 \) に等しい)
\( P,T,R \) は、それぞれ全圧[atm]、温度[K]、ガス定数[8.31451 J/mol/K]を示す。
\( \lambda_i,(i=1,l\ ) \) は、Lagrange乗数(非ゼロの一定値)で、未知数。 \( l\ \)は元素の種類の数。
\( n_j \) は、混合ガスに含まれる種 \( j \) のモル量
\( \alpha_{ij} \) は、化学種 \( j \) に含まれる元素 \( i \) の量論数
\( b_i^0 \) は、初期モル量から算出した元素\( i \) のモル量
各成分のGibbs自由エネルギー\( G_j^0 \) の計算は、DIPPRの物性定数・推算式を用いて、あるいはNASAの温度多項式を用いて推算することができる。
初期組成、温度、圧力を既知(Given)とすると、(26)から(28)式の \( n+l \) 個の式があり、未知数は、 出口平衡組成の \( n_j,(j=1,n) \) とLagrange定数 \( \lambda_i,(i=1,l\ ) \) の \( n+l \) 個となり、解くことができる。 ギブス自由エネルギーは温度のみの関数であり、出口平衡組成が(28)式の対数内にあり、非線形連立方程式となっている。 これを複数個の未知数をもつNewton法で収束させる。 このとき、出口組成が正である範囲を探す。 Lagrange定数は非ゼロの制約のみ(負でもよい)。
Topics 3:気液平衡の計算
ここでは、前述のTopics 1で紹介した3次の状態方程式を用いた高圧の気液平衡計算について紹介する。 液相が非理想溶液の場合には、液相の活量係数を用いた気液平衡計算が行われる。活量係数の推算にはWilson式、NRTL式などがあり、それぞれ二成分系のパラメータを必要とする。 また分子を構成するグループを用いるグループ寄与法UNIFAC、ASOGなどによる活量係数の推算方法もあり、2成分パラメータを必要としない場合もある。
大気圧を超える圧力下では、気液両相に状態方程式を適用し、気液平衡計算を行うことができる。 気液平衡状態では、ある成分の液相のフガシティー \( f_i^L \) と気相のフガシティー \( f_i^G \) とが等しい。 液相および気相のモル分率を、それぞれ \( x_i,y_i \) とし、液相および気相のフガシティー係数 \( \varphi_i^L, \varphi_i^G \) とすると、 \[ \left. \eqalign{ \begin{align*} f_i^L & = f_i^G, \quad & (i=1,N) \\ \varphi_i^L x_i & = \varphi_i^G y_i, \quad &(i=1,N) \\ \end{align*} } \right\} \tag{29} \] となる。成分数を \( N \) とした。
フガシティー係数を、3次の状態方程式から導出すると、SRK式、PR式それぞれ次の式となる。 SRK式のフガシティー係数は、圧縮係数 \( Z \) を用いて、 \[ \begin{align*} \ln \varphi_i = \ln \frac {f_i}{y_iP} & = \frac {b_i}{b}(Z-1) - \ln \Bigl[ Z(1- \frac bV) \Bigr] \\ & + \frac AB \Bigl[ \frac {B_i}B - \frac 2{a \alpha} \sum_j y_j(a \alpha)_{ij} \Bigr] \ln \Bigl( 1+ \frac BZ \Bigr) \tag{30} \\ \end{align*} \] となる。また、PR式のフガシティー係数は、 \[ \begin{align*} \ln \varphi_i = \ln \frac {f_i}{y_iP} & = \frac {b_i}{b}(Z-1) - \ln (Z-B) \\ & - \frac A{2 \sqrt {2}B } \Bigl( \frac {2 \sum_j y_ja_{ij}}a - \frac {b_i}b \Bigr) \ln \Bigl[ \frac {Z+(1+\sqrt {2})B}{Z+(1-\sqrt {2})B} \Bigr] \tag{31} \\ \end{align*} \] となる。ここで(30),(31)式に現れるパラメータは次のとおり、 \[ \left. \eqalign{ \begin{align*} a \alpha & = \sum_i \sum_j y_iy_j(a \alpha)_{ij} \\ b & = \sum_i y_ib_i \\ A & = \frac {(a \alpha)P}{(RT)^2} \\ B & = \frac {bP}{RT} \\ B_i & = \frac {b_iP}{RT} \\ \end{align*} } \right\} \tag{32} \] である。\( a_{ij},b_i \) などは臨界定数 \( P_c, T_c \)から算出できる。詳細は図書等1),を参照されたい。
いま2成分系を考える。成分毎の臨界定数が既知とすると、\( P,T \)を与えると、(24a),(25b)の状態方程式から気液の容積 \( V_m^G, V_m^L \) が計算できる。 そして圧縮係数 \( Z^L, Z^G \) が求められる。 そして、第 1成分の気液モル分率 \( x_1, y_1 \)を仮定し、 これらを(30),(31)式に代入することにより、気液のフガシティー係数 \( \varphi_i^L, \varphi_i^G \) が計算できる。 気液両相のフガシティーが等しくなるように、気液組成を収束させることにより、気相および液相組成を求めることができる。
もう少し数学的に取り扱うと、次の非線形連立方程式を解く問題に帰着できる。未知数は、\( P,T,x_1,x_2,y_1,y_2 \)の6個。式の数は 6個であり、解くことができる。ここで \( P_{spec},T_{spec} \) は、圧力・温度の指定値(入力値)を示す。 \[ \left. \eqalign{ \begin{align*} Obj_1 & = \sum_i x_i-1 = 0 \\ Obj_2 & = \sum_i y_i-1 = 0 \\ Obj_3 & = P - P_{spec} = 0 \\ Obj_4 & = T - T_{spec} = 0 \\ Obj_{4+i} & = \varphi_i^Lx_i - \varphi_i^Gy_i =0, \quad (i=1,2) \\ \end{align*} } \right\} \tag{33} \]
6つの変数のどれか2つを与えることで、残りの4つの変数を(33)式を用いて解くことができる。 連立非線形方程式の解法は、修正Newton法で解くことができる。下記演習問題を参照。
練習問題
ここでは状態方程式(SRK,PR)を用いた高圧系の気液平衡計算について練習問題を設定した。 上で述べたように非線形連立方程式を解くことになるが、数値解析:非線形方程式の項を参照されたい。 これら練習問題は既存の図書にある例題からピックアップした。
SRKの状態方程式
PRの状態方程式
物性・熱力学については、まだまだ取り上げるべきテーマは多い。反応器設計や反応器シミュレーションを実施する場合には物質や熱の移動現象を伴うことが多く、こうした移動現象は輸送物性が関与する。 また液液、気液など相間の物質移動の場合にも物質移動係数や熱移動係数の推算が必要となり、ガス吸収のヘンリー定数とか液相の拡散係数が必要であったりする。 これら必要な情報は今後、都度紹介したい。
Literature Cited
関連ファイルのダウンロードは、こちら(未リンク)で取り扱っています。
- 参考図書・文献
- 1) Poling,B.E.,J.M.Prausnitz,J.P.O'Connell:"The properties of gases and liquids",5th Ed.,McGraw-Hill(2001).
- 2) Zehe,M.,S.Gordon,B.J.McBride:NASA/TP-2001-210959/Rev1,Feb.(2002).[L2911]
- 3) ftp://ftp.technion.ac.il/pub/supported/aetdd/thermodynamics
からダウンロード(現在時点ではつながらない)。NASA polynomialsで検索し、BurcatのHPからダウン可能。 - 4) Burcat,A. and B.Ruscic: ANL-05/20,TAE 960(2005). (Argonne national laboratory)
- 5) "NIST-JANAF Thermochemical Tables",Ed. M.W.Jr.Chase,Amer.Inst.Phys.(1998).
- 6) Joback,K.G. and R.C.Reid:Chem.Eng.Commun.,57,233-243(1987).[L4978]
- 7) Constantinou,L. and R.Gani: AIChE J.,40,(10),1697-1710(1994).[L4971]
- 8) Constantinou,L.,R.Gani and J.P.O'Connell:Fluid Phase Equil.,103,11-22(1995).[L4981]
- 9) Domalski,E.S. and E.D.Hearing: J.Phys.Chem.Ref.Data,22,805-1159(1993).[L5009]
- 10) Ruzicka,V. and E.S.Domalski:J.Phys.Chem.Ref.Data,22,597-618(1993).[L5064]
- 11) Ruzicka,V. and E.S.Domalski:J.Phys.Chem.Ref.Data,22,619-657(1993).[L5065]
- 12) Gmehling.J.,J.Menke,J.Kfafczyk and K.Fischer:"Azeotropic Data",Wiley-VCH(2004).
- 13) Benson,S.W.:"Thermochemical Kinetics",John Wily & Sons,N.Y.(1968).
- 14) Redlich,O. and J.N.S.Kwong:Chem.Rev.,44,233(1949).
- 15) Soave,G:Chem.Eng.Sci.27,1197(1972).
- 16) Peng,D.-Y.,D.B.Robinson:I.E.C.,Fundam.,15,1,59(1976).[L0504]
- 17) 荒井、宮本、亀山、山口:「新体系化学工学 計算機化学工学」、オーム社(1992).[L5108]
- L2982) (Internet Download)
- L2985) Gordon,S. and B.J.McBride: NASA Tech.Report SP-273(1976).
