トップ > ライブラリ > 数値解析 > 微分方程式

数値解析：微分方程式

現在工事中です。 取り敢えず繋がりましたが、これからも更新する予定です。

先頭に戻る

【注】数式表示にはMathJaxを利用しています。IE8以下では表示が遅くなる可能性があります。FireFox などIE8以外のブラウザを利用下さい。

微分方程式の概要

ここでは独立変数がひとつ、従属変数がひとつの、一元一階の常微分方程式の解法について、総括する。 また同じく独立変数が複数で、従属変数がひとつの偏微分方程式の解法についても総括する。これら微分方程式の解法の多くは独立変数を計算領域でメッシュに分割し、差分化して解くことをしている。 実際のエンジニアリング業務ではこうした単純な微分方程式となることはそれほど多くないが、 工学的には高階の連立常微分方程式や連立の偏微分方程式となることが多い。

高階の常微分方程式は、変数変換により連立の一階の常微分方程式に変換できる。 \[ \begin{align*} \frac {d^ny}{dt^n} & = f \Bigr( t, y, y', y'', \cdots, \frac {d^{n-1}y}{dt^{n-1}} \Bigr) \tag{1} \end{align*} \]

このとき、変数変換 \[ \left. \eqalign{ \begin{align*} y_1 & =y, \\ y_2 & =\frac {dy_1}{dt}= \frac{d^2y}{dt^2}, \\ & \cdots \\ y_n & =\frac {dy_{n-1}}{dt}= \frac {d^{n-1}y}{dt^{n-1}} \\ \end{align*} } \right\} \tag{2} \]

により、n元一階の連立常微分方程式が得られる。

連立微分方程式および連立偏微分方程式の実際の、詳細な解法については、こちら、数値解析：連立微分方程式を参照されたい。また差分法の基礎的事項および差分法による微分方程式の 解法については、こちら、数値解析：有限差分法でも述べる。化学工学で使われる有限差分法は、こちら、技術計算：有限差分法を参照されたい。

以下、微分方程式を解く上での基礎的事項について解説する。また工学的に頻出する微分方程式の解法については、連立微分方程式のところも参照されたい。ここでは極めて初歩的な知見を紹介し、より具体的・実際的な話題は連立微分方程式のところで解説する。

先頭に戻る

常微分方程式

陽解法

一元一階の次の常微分方程式を考える。 \[ \begin{align*} \frac {dy}{dt} & = f \{ t, y(t) \} \tag{3} \end{align*} \]

一階の常微分方程式を解くとき、ひとつの初期条件または境界条件を必要とする。 いま簡単のため、初期条件を与えて解くことを考える（初期値問題という）。初期条件 \( t = t_0 \) を次式で与える。 \[ \begin{align*} y(t_0) & = y_0 \tag{4} \end{align*} \]

初期値問題を解くとき、有名な方法として、Runge-Kutta法やRunge-Kutta-Gill法がある。 その他にも、Euler法、Milne法、Adams法など多数の解法が利用できる。

いま nステップ目である独立変数 \( t_n \)点まで解 \( y_n \)が求められたとし、刻み幅hを隔てた次の点 \( t_{n+1}=t_n+h \)の従属変数の値 \( y_{n+1} \) を予測することを考える。 Euler法 (Forward Euler method、陽解法のEuler法) では、次式で予測される。 \[ \begin{align*} k_1 & = h f(t_n,y_n) \\ y_{n+1} & = y_n + k_1 + O(h^2) \\ & {\rm then} \\ y_{n+1} & = y_n + h f(t_n,y_n) + O(h^2) \tag{5} \end{align*} \]

また４次のRunge-Kutta法では、次式で予測される。 \[ \left. \eqalign{ \begin{align*} k_1 & = h f(t_n,y_n) \\ k_2 & = h f(t_n+ \frac h2,y_n+ \frac{k_1}2 ) \\ k_3 & = h f(t_n+ \frac h2,y_n+ \frac {k_2}2 ) \\ k_4 & = h f(t_n+h,y_n+k_3) \\ y_{n+1} & =y_n + \frac 16 ( k_1 + 2k_2 + 2k_3+k_4) + O(h^5) \\ \end{align*} } \right\} \tag{6} \]

式(6)の右辺の関数形 \( f(t,y) \) は通常与えられ、上から順番に \( k_1,\cdots, k_4, y_{n+1} \)と代数的にストレートに求めることができる。関数 \( f(t,y) \)を４回計算することで次の点を予測することができる。 このように収束・反復計算もなく、直接、次の分割点の値を計算する方法を陽解法 (Explicit Method) という。陽解法は、アルゴリズムが単純で、計算が速い特徴がある。一方、分割刻みの与え方や与えられた微分方程式によっては 解が発散することがある。自動刻み幅を採用するRunge-Kutta法などもあるが、陽解法を採用する限り、解の安定性の問題が残る。

化学工学分野で、例えば重合反応のような発熱反応を、バッチ式反応器で行うことを考える。除熱装置が時刻ゼロで故障すると、反応による発熱が起こり、温度が次第に上昇し、遂には暴走反応が起きる。このシミュレーションを、Forward Euler法や4次精度のRunge-Kutta法で解くと 場合によっては、転化率100%を突き抜けてしまったり、天井温度（装置内の反応物質がすべて反応し発熱したときに到達する最高温度）を越えてしまうことを経験する。逆に、反応速度定数（例えば頻度因子と活性化エネルギー）を実験データから最小二乗するとき、 頻度因子や活性化エネルギーの初期値を与え、実験値と合致するような値を探索するが、探索途中で 頻度因子や活性化エネルギーの値が大きく振れるため、暴走反応に近い条件で計算することもある。このとき陽解法を採用していると解の安定性や精度に問題があるため、 最適値が得られない可能性がある（計算機のOverflowやゼロ割で途中でストップすることもある）。

先頭に戻る

陰解法

安定して微分方程式を解くためには、陰解法（Implicit Method) と呼ばれる解法を使うことが望ましい。陰解法を用いると、コードが複雑化し、反復計算となることが多いが、解の安定性や精度上の問題は陽解法に比較して圧倒的に少ない。 陰解法を適用した、Euler法 (Backward Euler Methodという）では次式を解くことになる。 \[ \begin{align*} y_{n+1} & = y_n + h f(t_n+h,y_{n+1}) + O(h^2) \tag{7} \end{align*} \]

陽解法のEuler法の(5)式とは右辺第２項が違う。右辺第２項は次の時間ステップ \( t_n+h \equiv t_{n+1} \) での変数値 \( y_{n+1} \) が入り、(5)式と違い、関数 \( f(t,y) \) の形にもよるが、代数的に解けない。 関数が簡単な形以外（簡単な形のときは解析的に微分方程式自体が解けることが多く、Runge-Kutta法などにより積分する必要がない）は収束・反復計算となる。

陰解法のRunge-Kutta法 L1365,L2906)もあるが、ここではBackward Euler法を適用して微分方程式を解くことを考える。いま独立変数 t の解析空間を範囲 [t1, t2]とし、この間で微分方程式を解くことを考える。この区間を幅 h で等間隔に N個のメッシュに刻む。格子点は t1の点を1とし、t2の点がN+1となる。格子点での関数値を \( y_1, \cdots, y_{N+1} \) とすると、(7)式は \[ \begin{align*} y_{1,n+1} & = y_{1,n} + h f(t_{1,n+1},y_{1,n+1}) \tag{8a} \\ \cdots \\ y_{j,n+1} & = y_{j,n} + h f(t_{1+jh,n+1},y_{j,n+1}) \tag{8b} \\ \cdots \\ y_{N+1,n+1} & = y_{N+1,n} + h f(t_{2,n+1},y_{N+1,n+1}) \tag{8c} \\ \end{align*} \]

と、関数 \( f(t,y) \)の形にもよるが \( y_1, \cdots, y_{N+1} \) を独立変数とする非線形の連立方程式に帰着する。 添え字 n, n+1 はそれぞれ n回目および n+1回目の反復の値であることを示す。 この非線型連立方程式をNewton法により線形化し、反復・収束計算で解くことができる。関数 \( f(t,y) \) の形が単純であれば 線形連立方程式となり、反復計算することなくダイレクトに解を得ることができる。

非線型連立方程式のところでも述べたように、Backward Euler法では隣接した格子点だけが現れ、ヤコビ行列はバンド行列となる。

例題１：バッチ反応器による１次反応（陽解法）

バッチ式反応器で、初期濃度 C0で濃度 Cについて1次の反応を考える。反応速度は \( r = kC \) とする。このとき反応器内の転化率を \( x=1 - C/C_0 \) とすると、反応器内の転化率変化は次式で表される。 \[ \begin{align*} \frac {dx}{dt} = k (1-x) \tag{101} \end{align*} \] これを、Forward Euler法（陽解法）で解きなさい。反応速度定数 k[1/hr]を 0.26のときおよび0.75のときの２ケースを、時間刻み h=1.0 [hr]とし、0から10hrまで解きなさい。 なお上式は解析的に解くことができ、次式が解析解である。数値解との残差も出力しなさい。 \[ \begin{align*} x = 1- \exp( -kt ) \tag{102} \end{align*} \]

例題２：バッチ反応器による１次反応（陰解法）

例題１のバッチ反応器の非定常問題を、Backward Euler法で解きなさい。なおパラメータωを導入し、ω=1のときFull Implicit、ω=0のときExplicitとなるようコードを作成しなさい。 \[ \begin{align*} \frac {x^{n+1}-x^n}{h} = k [ 1- \{ \omega x^{n+1} +(1- \omega) x^n \} ] \tag{103} \end{align*} \]

上の例題１および例題２のとき、反応速度定数 kを0.26とし、時間ステップ hを4.0hrとしたときの解析解を図１に示す。 この計算例では陽解法の不安定性を明示するため、わざと時間ステップを粗くしている。

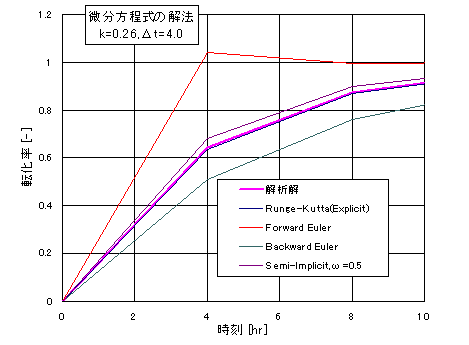
図１：解法の比較

図１の凡例は次のとおり。

陽解法のオイラー法は、時間ステップのとり方により、転化率が1.0を越えてしまい、解の不安定性や精度が悪い。 同じ陽解法の4次精度Runge-Kutta(RK)法では、時間ステップ 4.0 ではまだオイラー法に見られる不安定性は見られない。時間ステップや反応速度定数の値により、RK法でも不安定領域となる可能性がある。 一方、陰解法のオイラーおよび半陰解法のオイラーでは解の精度はRK法より劣るが、陽解法の不安定性は解消されていることがわかる。

上の例題では、反応速度定数を0.26と固定しているが、暴走反応のように温度の急上昇が起こると反応速度定数はべき級数的の増加し、数百倍、数千倍になり陽解法の不安定性がより顕著に現れることがある。時間刻み幅を反応速度定数の値により適切に制御しないと不安定となる。 反応速度定数を実験データから最適化（最小二乗）するとき、頻度因子や活性化エネルギーの値を大きく変動させて最適化を行うが、微分方程式の解法に陽解法を採用するとなかなか収束しなかったり、発散する、またはゼロ割やオーバーフローの原因となることが多い。 従ってコードを作成する最初のハードルは高い（コードが複雑化する）けれど、陰解法による解き方を採用することで、後の計算の安定性に大きく貢献する。

先頭に戻る

境界値問題

いままでは初期条件 \( t=0 \) のときの値、すなわち初期値 \( y(0) \) を与えてきた。しかし問題によっては終点 (End Point) での関数値が与えられることもある。あるいは終点での微係数が境界条件として与えられることがある。 また終点でなく、途中の点での条件を与えられることがある。 陽解法を使い、初期値を仮定し、終点での値が一致するまで、初期値を修正し、反復計算とする方法（試行錯誤法）がよく利用される。しかしながら、この方法では解の収束安定性に不安が残る。

一方、陰解法を用いると、前述の(8)式に示したように連立（非）線形方程式に帰着させることができる。 そのため終点境界の値を設定することは容易である。また微係数を設定することも容易にできる。 例えば終点の値、t=t2で境界条件 \( y_{N+1}=y_{\rm {end point}} \)を取るとすると、(8c)式の代わりに次式を使えはよい。

\[ \begin{align*} & y_{N+1,n+1} = y_{\rm {end point}} \tag{9a} \\ & {\rm Obj} = y_{N+1,n+1}-y_{\rm {end point}} = 0 \tag{9b} \\ \end{align*} \]

同じように、中間の点の値を境界条件とするときも、(7)式とN+1の代わりに格子点 jを代入した式を採用すればよい。

先頭に戻る

スティッフな微分方程式

連立微分方程式の中には、"Stiffな微分方程式"（日本語で「硬い微分方程式」）と呼ばれる特殊な微分方程式が存在する。通常の陽解法はもちろん、ステップ幅可変の陽解法でも解くことが難しい微分方程式問題である。 化学工学では、気相でのメタン燃焼（メタンの酸化反応）のようにラジカル種の素反応を考慮する場合、その素反応の数が数十から百数十存在し、その反応速度が極めて速い反応から遅い反応まで同時に混在する問題を解くとき、Stiffな微分方程式に相当する。

同様に２つの並列反応があり、片方の反応が早く、残りが遅いとき、速い反応に合わせて固定時間刻みを小さくすると、遅い反応を解くのに極めて膨大なステップ数を経ないと解に到達しないことがある。可変刻みで解くこともあるがこのような特異な微分方程式 をとくのは厄介な問題に相当する。

こうしたStiffな微分方程式を解くための特殊な解法が、種々用意されている。基本的には可変ステップ幅を用い、陰解法もしくは半陰解法を用いた解法が多い。これら解法の比較や スティッフな微分方程式の解法の詳細については、別のところで取り扱っています。詳しくはそちらを参照して下さい。

先頭に戻る

偏微分方程式

独立変数が２つ以上のときの微分方程式（偏微分方程式）の解法について基礎的事項について以下述べる。工学的・実用的な視点からの解法は連立微分方程式の項を参照されたい。

偏微分方程式の分類

２変数 x,y の２階線形偏微分方程式を考える。 \[ \begin{align*} au_{xx}+bu_{xy}+cu_{yy}+du_x+eu_y+fu=g \tag{10} \end{align*} \]

判別式 \( b^2-4ac \) が、正のとき双曲型(hyperbolic)、ゼロのとき放物型(parabolic)、負のとき楕円型(elliptic)偏微分方程式と分類される。

化学工学分野では、非定常の拡散方程式などは放物型がよく見られる。流体解析のとき圧力のPoisson方程式など楕円型偏微分方程式も割合に現れる。 双曲線型はそれほど多くなさそうに思われる（今までの経験で出現したのを見たことがない）。

先頭に戻る

放物型偏微分方程式

２つの独立変数 t,y とし、従属変数を Tとするとき、放物型偏微分方程式の典型例として、次の非定常の拡散方程式(11)式と、線形Burgers方程式と呼ばれる(12)式とが化学工学分野でよく現れる。 \[ \begin{align*} & \frac{\partial T}{\partial t} = \alpha \frac{\partial ^2 T}{\partial y^2} \tag{11} \\ & \frac{\partial T}{\partial t} + u \frac{dT}{dy} = \nu \frac{\partial ^2 T}{\partial y^2} \tag{12} \\ \end{align*} \]

Burgers方程式は、運動量方程式と呼ばれるもので左辺第２項の移流項が非線型となっていることに特徴がある。移流項のy方向速度uをゼロとすると拡散方程式に等しくなる。

先頭に戻る

楕円型偏微分方程式

楕円型偏微分方程式として、典型的なLaplaceの方程式(13)、Poisson方程式(14)がある。 \[ \begin{align*} & \frac{\partial^2 T}{\partial x^2} + \frac {\partial^2 T}{\partial y^2} =0 \tag{13} \\ & \frac{\partial^2 T}{\partial x^2} + \frac {\partial^2 T}{\partial y^2} =f(x,y) \tag{14} \\ \end{align*} \]

Lapalaceの方程式はPoisson方程式の右辺をゼロを置いた場合に相当し、Poisson方程式と同じ解法が利用できる。

先頭に戻る

偏微分方程式の一般的な解法

上述した偏微分方程式は、通常解析的に解くことができない。従って何らかの数値解法を用いて解くことを行う。一般に差分近似を用いた差分法が用いられることが多い。 差分法を適用するとき、解析領域を格子状に刻み格子点（メッシュ点またはグリッドという）を生成し、支配方程式（境界条件を含む）を格子点上の従属変数で置き換える操作（離散化、discretisation）を行う。 メッシュの作成については別のところ（例えば数値解析：有限差分法）にて詳述する。

離散化された方程式は、グリッド点数だけ未知数をもつ連立方程式を構成している。普通は非線型連立方程式となっており、これを各種の収束手法を用い、数値計算で解くことを行う。 三次元直交座標系で、各方向に100個の格子点で刻むと、合計1003=106（=１メガ)元の連立方程式となる。線形の連立方程式と考え、行列・ベクトルで表すと、 \[ \begin{align*} {\bf A}{\bf x} = {\bf b} \tag{14} \end{align*} \]

なる。行列 Aは正方行列であり、行列要素を保存するため1012（1000ギガ = 1テラ）個の配列が必要となる。Fortranの倍精度実数（8バイト）を使うと 8TBのメモリを専有することになる。 この値は現在のHDDの1台の容量が4TB程度であることを考えれば、天文学的な値であり、直接解く（係数行列をひっくり返して解く）ことは実現不可能であることがわかる。 計算機能力が発達してきたとはいえ、部分的に解き、反復することにより全体を解くことをせざるをえない。

繰り返し反復計算を実施することから、解を得る方法に陽解法（Explicit Method）と陰解法（Implicit Method）が偏微分方程式を解く上でも存在する。

以下、放物型と楕円型偏微分方程式の解法について、例題を交えて詳述する。

先頭に戻る

放物型偏微分方程式の解法

解法を簡単に解説するため、もっとも単純な非定常の拡散問題（放物型偏微分方程式に相当）を取り上げ、数値計算方法を以下解説する。 取り上げる例題として無限平板内の非定常温度分布問題（例題１）を考える。

xy平面に平行な厚さ 2単位の平板を考える。初期に温度 1単位の平板を時刻ゼロで瞬時に温度 0単位の空間に浸す。このとき平板内の温度分布の時間変化を求める問題である。 座標原点を平板の中央とし、厚み方向を z軸とする。このときの支配方程式は次式となる。 \[ \begin{align*} \frac{\partial T}{\partial t} & = \alpha \frac{\partial ^2 T}{\partial z^2} \tag{15} \\ \end{align*} \]

ここでαは無次元化された熱伝導度である。t,z,Tも無次元化されているとする。

解析方法は差分法を使う。差分法を適用するため、解析領域をメッシュに分割する必要がある。

先頭に戻る

陽解法

差分法でも、上の常微分方程式で述べたように陽解法と陰解法とがあり、陽解法では収束安定性に問題があり、陰解法が望ましいことは偏微分方程式でも同様である。 ここではまず解析コードが単純な陽解法について解説する。もっとも簡単な直交座標系の一次元非定常熱伝導方程式、例題３を考える。

例題３：１次元非定常熱伝導の解析（陽解法）

次の非定常熱伝導式（無次元化されている）を初期条件および境界条件のもとで、差分化し、Forward Euler法で解きなさい。FortranコードまたはXlsのVBA上のBasicコードで解きなさい。 \[ \begin{align*} \frac{\partial T}{\partial t} & = \alpha \frac{\partial ^2 T}{\partial z^2} \tag{A1} \\ {\rm IC:} \quad T & =1.0 \quad {\rm at~ t=0,~ at~ any~ z} \\ {\rm BC1:} \quad \frac{\partial T}{\partial z} & = 0.0 \quad {\rm at~ any~ t,~at ~ z=0} \\ {\rm BC2:} \quad T & =0.0 \quad {\rm at~ any~ t, at ~ z=1} \\ \end{align*} \]

(1) 解析領域0～1の範囲を20等分する。(Δz=0.05)
(2) 時間刻み0.01で、100ステップまで求める(Δt=0.01)
(3) 有効熱伝導度は0.1とする。(α=0.1)
(4) 中心（z=0)での温度分布の時間変化を、解析解と比較しなさい。
(5) α=0.2として、計算実行しなさい

従属変数として温度を採用すると熱伝導方程式に、濃度とすると拡散方程式になるが、ここでは温度を従属変数とみなす。 この例題を解く上でヒントは次に示すとおり。なお(A1)式で表される偏微分方程式は変数分離型をしており、解析的に解くことができる。

例題３のヒント

解析解5)は、次式となる。 \[ \begin{align*} T(t,z) = \frac4\pi \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)} \cos \Bigl\{ \frac {(2n+1)\pi}{2}z \Bigr\} \exp \Bigl\{ -\frac {(2n+1)^2\pi^2\alpha}{4}t \Bigr\} \tag{A2} \end{align*} \]

(1) z=0より小さいところに、仮想の格子点-1を考慮し、境界条件１を考慮する。
(2) VBAの"forward_euler"ルーチンを作成しなさい。
計算結果をシートのセルに転送する出力サブルーチンほかを、開発しなさい。
(3) マクロ実行ボタンを作成し、ボタンクリックでForward_Eulerが実行するようコードを作ると便利。

このヒントから、解析領域である空間の z座標の範囲 [0,1] の範囲をメッシュに分割する。 この例題では刻み幅0.05の等分割で格子生成する。z=0の格子点の外側、つまりz=-0.05の位置に仮想のグリッド点-1を考慮し、コードを作成する。

支配方程式(15)式を差分で近似する。左辺の時間微分は前進差分（Forward Euler）、右辺の空間微分は中心差分を適用する。上付添字 nは時間ステップを、下付添字 jは格子点をそれぞれ示す。 \[ \begin{align*} \frac {\partial T}{\partial t} & = \frac {T_j^{n+1}-T_j^n}{\Delta t} \tag{16} \\ \frac {\partial ^2 T}{\partial z^2} & = \frac {T_{j-1}^n-2T_j^n+T_{j+1}^n}{\Delta z ^2} \tag{17} \\ \end{align*} \]

これらを(15)式に代入整理すると(18a)式が得られる。また2つの境界条件も、差分化すると(18b),(18c)式が得られる。 \[ \begin{align*} & T_j^{n+1} = T_j^n + \alpha \frac {\Delta t}{\Delta z^2} (T_{j-1}^n-2T_j^n+T_{j+1}^n) \tag{18a} \\ & T_{-1}^n = T_{1}^n \tag{18b} \\ & T_{N}^{n+1} = 0.0 \tag{18c} \\ \end{align*} \]

図２：陽解法の結果

図３：中心z=0の温度（α=0.1とα=0.2）

(18b)式はz=0の外側の格子点-1の温度はz=0のひとつ内側の格子点+1の温度に等しいということを示す。この関係を、j=0と置いた(18a)式に適用すると、平板中心の 次の時間ステップの温度 \( T_0^{n+1} \)の値を求めることができる。(18a)式をj=0からj=N-1まで計算し、j=N点は(18c)を使うことで、n+1回目の値をすべて得ることができる。

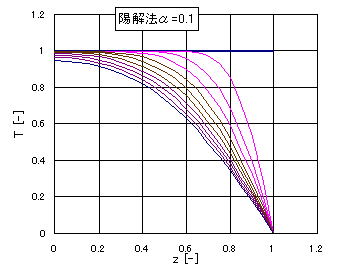
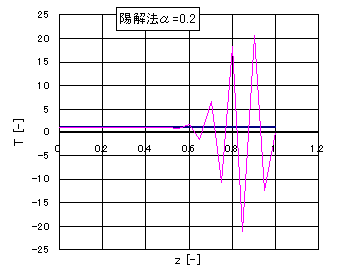
計算をはじめるにあたり、初期条件(n=0)の各格子点の値 \(( T_j^0=1, j=0,N )\)を与えることにより、(18)式から \(( T_j^1,j=0,N )\)の値を次々に計算することができる。 以上が陽解法による解法である。α=0.1のときの陽解法の結果を図２に示す。Δt=0.01で解いたとき、t=0でT=1の温度が次第に低下する様子がわかる（t=0.1,0.2,･･･1.0の温度分布をプロットしている）。 また図３はα=0.2としたとき、t=0.1（ピンクの線）で温度分布が振動してしまい、正しい解を与えていないことがわかる。

(18a)式を見ると格子点 jの温度を計算するとき、j-1点の温度 \( T_{j-1}^{n+1} \) は直前の計算で求められており、この最新の値を用いて計算することも可能である。ただしj=0から順番に昇順で計算する場合に限る。 \[ \begin{align*} & T_j^{n+1} = T_j^n + \alpha \frac {\Delta t}{\Delta z^2} (T_{j-1}^{n+1}-2T_j^n+T_{j+1}^n) \tag{19} \\ \end{align*} \]

(19)式は、右辺にn+1回目の値が一部利用されることから、半陰解法(Semi-implicit)とも呼ばれる。

先頭に戻る

陰解法

次に陰解法による解き方を解説する。陰解法は空間微分項にn+1回目の値を使う。すなわち(17)式の代わりに次式を使う。 \[ \begin{align*} \frac {\partial ^2 T}{\partial z^2} & = \omega \frac {T_{j-1}^{n+1}-2T_j^{n+1}+T_{j+1}^{n+1}}{\Delta z^2} + (1-\omega) \frac {T_{j-1}^n-2T_j^n+T_{j+1}^n}{\Delta z^2} \tag{20} \\ \end{align*} \]

ここでω=1のとき完全陰解法(Full Implicit)を、ω=0のとき陽解法となる。ω=0.5のときCrank-Nicholson法（半陰解法）となる。コードを作成するときはパラメータωを入力するときExplicit、Implicitを切り替えられるためコードの汎用性が広がる。 この式を基礎式および境界条件に代入し、整理すると(21)式が得られる。

\[ \begin{align*} -c \omega T_{j-1}^{n+1} & +(2c \omega +1) T_{j}^{n+1}-c \omega T_{j+1}^{n+1} = \\ & c (1-\omega) T_{j-1}^n +\{1-2c (1-\omega) \} T_j^n+ c(1-\omega) T_{j+1}^n \tag{21a} \\ & {\rm where} \quad c= \frac {\alpha \Delta t}{\Delta z^2} \\ (2c \omega +1) T_{0}^{n+1}- & 2c \omega T_{1}^{n+1} = \{1-2c (1-\omega) \} T_1^n+ 2c(1-\omega) T_{1}^n \tag{21b} \\ T_{N}^{n+1} = 0.0 \tag{21c} \\ \end{align*} \]

(21)式は、変数 \( T_j^{n+1},j=0,N \)を未知数とする連立線形方程式となっている。また格子点 (21a)式から分かるように前後の格子点のみに依存する。 連立線形方程式を行列表示したとき、係数行列 Aは対角要素とその上および下の三列に要素が現れる三行対角行列（tridiagonal matrix)となっており、ガウスの消去法 を用いて簡単に、ストレートに解くことができる（後述のThomas法）。

例題４：例題３を陰解法で解く

例題３をBackward Euler法で解きなさい。ただし拡散項はCrank-Nicholson法を使用すること。

Tridiagonal Matrixのソルバーはm_thomas.for(FORTRAN言語用）を使うこと。

リスト１：m_thomas.for 

C-----------------------------------------------------------------------
C
C  ３行対角行列をもつ連立１次方程式を、THOMAS法（ガウス消去法）で解く
C
C  出典：榊原オリジナル
C
C 引数：
C  NMAX: (in)   INT*4  配列A,B,C,Dの最大要素数。
C     A: (in)   REAL*8 下対角行列の要素を入れた１次元配列
C     B: (in)   REAL*8 対角行列の要素をいれた１次元配列
C     C: (in)   REAL*8 上対角行列の要素を入れた１次元配列
C     D: (in)   REAL*8 右辺のベクトル。１次元配列。解が格納され、戻される
C   P,Q: (work) REAL*8 作業用１次元配列
C    NZ: (in)   INT*4  未知数の数
C
      SUBROUTINE   M_THOMAS( NMAX,A,B,C,D,P,Q,NZ )
CDEC$IF DEFINED (DLL)
CDEC$ATTRIBUTES DLLEXPORT::M_THOMAS
CDEC$ENDIF
C
C  TRIDIAGONAL MATRIX
C
CDEC$IF DEFINED (DLL)
      INCLUDE      'COMMON01.H'
CDEC$ELSE
      INCLUDE      'COMMON.H'
CDEC$ENDIF
      DIMENSION    A(NMAX),B(NMAX),C(NMAX),D(NMAX),P(NMAX),Q(NMAX)
C
      IERR=0
      P(1)=C(1)/B(1)
      Q(1)=D(1)/B(1)
      DO J=2,NZ
        W=ONE/(B(J)-A(J)*P(J-1))
        IF(MONI.GE.5) WRITE(NMONI,*) ' J = ',J
        P(J)=C(J)*W
        Q(J)=(D(J)-A(J)*Q(J-1))*W
      END DO
      D(NZ)=Q(NZ)
      DO J=1,NZ-1
        JJ=NZ-J
        D(JJ)=Q(JJ)-P(JJ)*D(JJ+1)
      END DO
      RETURN
      END SUBROUTINE M_THOMAS

サブルーチンm_thomas.for（Tridiagonal Matrix Solver）の引数の与え方は配列Bに対角要素、Aに対角下、Cに対角上、Dに右辺ベクトルをセットする。NMAXは配列の定義要素数、NZは実際の未知数の数、 P,Qは作業用の配列である。得られた解はD配列に格納され戻される。

図４：三行対角行列

例題５：例題４によるケーススタディ

例題４で作成したコードを用い、次のケースを計算しなさい。

(1) α=とし、陽解法（ω=0）で解く。（発散してしまうことを確認）
(2) α=とし、完全陰解法（ω=1）で解く。（収束することを確認）
(3) α=とし、Crank-Nicholson法（ω=0.5）で解く。（収束することを確認）

例題５で作成したコードを用い、計算させた結果を表示する。

図５：陰解法（α=0.2）の結果

図６：中心温度の比較

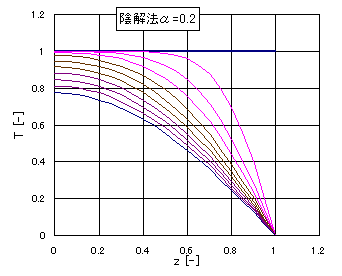
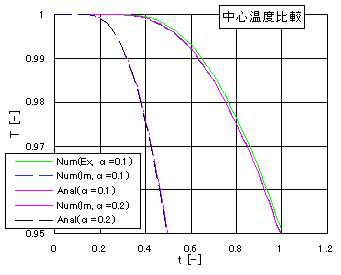
α=0.5としたとき、時間刻みを0.01とした陰解法による温度分布の時間変化を図５に示す。各曲線はΔt=0.1ごとの分布を示す。陽解法に比べ、ほぼ正常にまた安定して解が得られている。 また平板中心z=0 の温度の時間変化を図６に、α=0.1のときおよびα=0.2のときの陰解法(Im)の数値解と解析解との比較を行った。解析解と数値解とはほぼ一致している。 また図６にはα=0.1のときの陽解法（Ex）の数値解もプロットした。陽解法は解析解からやや離れており、計算精度が陰解法より劣ることがわかる。

なお陰解法はω=0.5としたCrank-Nicholson法を採用した。

以上の計算例でもわかるように、放物型偏微分方程式を解くときにも陽解法の安定性に問題があり、陰解法を採用することにより刻み幅の制限は大幅に緩和されることがわかる。

Burgers方程式(12)式も同様に差分化し、陽解法および陰解法を用いて解くことができる。Burgers方程式を離散化するとき、 次のクーラン数 C、および格子レイノルズ数Reが現れる。そしてこれら無次元数の比C/Reは、非定常拡散方程式の差分化式(21a)の係数cに一致する。 \[ \begin{align*} {\rm C} & \equiv \frac {u \Delta t}{\Delta z} \tag{22} \\ {\rm Re} & \equiv \frac {u \Delta z}{\alpha} \tag{23} \\ c & = \frac {\rm C}{\rm Re} = \frac{\alpha \Delta t}{\Delta z^2} \tag{24} \\ \end{align*} \]

Burgers方程式を陽解法（前進オイラー法）で安定して解くためには、次のクーランの安定条件（必要条件）を満足する必要がある2)。 \[ \begin{align*} \Delta t & < \frac {\Delta z}{|u|} \tag{25} \\ \Delta t & < \frac {\Delta z^2}{2 \alpha} \tag{26} \\ \end{align*} \]

また時間刻み幅は、ハートの条件（十分条件）を満足する必要がある2)。 \[ \begin{align*} \Delta t & < \frac {2 \alpha}{u^2} \tag{27} \\ \end{align*} \]

例題３のΔz=0.05、Δt=0.01、α=0.2では、C/Re = 0.8 となる。(26)式の条件 C/Re < 0.5を越えており、不安定領域であることがわかる。

Burgers方程式の解法については、連立微分方程式のところで述べる。

演習問題１（応用問題）：球座標系の拡散方程式

球座標系の次の無次元化された拡散方程式（熱伝導度式）を、与えられた境界条件下で差分化し、Backward Euler法で解きなさい。m_thomas.forを使うこと。 \[ \begin{align} \frac{\partial T}{\partial t} & = \alpha \biggl\{ \frac {1}{r^2} \frac{\partial}{\partial r} \biggl( r^2 \frac {\partial T}{\partial r} \biggr) \biggr\} \tag{A3} \\ {\rm IC:} \quad T(0,r) & =1 \\ {\rm BC1:} \quad \frac {\partial T}{\partial r} & = 0 \quad {\rm at~ r=0,~ at ~ any ~ t} \\ {\rm BC2:} \quad T(t,1) & = 0 \\ \end{align} \]

【条件およびヒント】

(1) 半径１の初期温度 \( T_{\rm ini} \) 、表面温度 \( T_{w} \) の球粒子内の温度分布の解析解は次式で与えられる。
\[ \begin{align*} \frac {T-T_{\rm ini}}{T_w-T_{\rm ini}} = 1 + \frac2{\pi r} \sum_{n=0}^\infty \frac{(-1)^n}n \sin(n \pi r) \exp(- n^2 \pi^2 \alpha t) \tag{A4} \end{align*} \] (2) 有効熱伝導度α（無次元）は、0.01とする。
(3) ｒ方向の分割数として20を使う。
(4) Δｔ=0.01として、100ステップまで計算しなさい。
(5) 基礎式(79)の右辺を展開し、二階微分項と一階微分項とに分解する。二階微分項には、2次精度の差分で、また、一階微分には２次精度の差分で近似し、Crank-Nicholonスキームで陰解法、陽解法ともに解けるよう、パラメータβを導入しなさい。β=1のとき、Full Implicit、β=0のときExplicit、β=0.5のときCrank-Nicholson陰解法となる。
\[ \begin{align} \frac{\partial ^2 T}{\partial r^2} & = \beta \frac{T_{j+1}^{n+1}-2T_{j}^{n+1}+T_{j-1}^{n+1}}{\Delta r^2} +(1-\beta) \frac{T_{j+1}^{n}-2T_{j}^{n}+T_{j-1}^{n}}{\Delta r^2} \tag{A5} \\ \frac{\partial T}{\partial r} & = \beta \frac{T_{j+1}^{n+1}-T_{j-1}^{n+1}}{2 \Delta r} +(1-\beta) \frac{T_{j+1}^{n}-T_{j-1}^{n}}{2 \Delta r} \tag{A6} \\ \end{align} \]

先頭に戻る

楕円型偏微分方程式の解法

楕円型偏微分方程式として、Poissonの方程式を取り上げる。放物型と同様格子を刻み、差分法で解くことを考える。 \[ \begin{align*} \frac{\partial^2 T}{\partial x^2} + \frac {\partial^2 T}{\partial y^2} =f(x,y) \tag{14} \\ \end{align*} \]

２階微分を中心差分に置き換える。x,y方向の刻み点をそれぞれi,jとし、(i,j)格子点での従属変数値を \( T_{i,j} \)とする。また(14)式の右辺値を \( f_{i,j} \) とすると、 (14)式を差分化した式は、次式となる。 \[ \begin{align*} \frac {T_{i-1,j}-2T_{i,j}+T_{i+1,j}}{\Delta x^2} + \frac {T_{i,j-1}-2T_{i,j}+T_{i,j+1}}{\Delta y^2} = f_{i,j} \tag{28} \\ \end{align*} \]

図７：計算領域

境界条件は、図７に示す計算領域の外周で与えられる。そして(28)式は、全格子点を未知数とする線形の連立方程式になっている。 格子点の数が少なければ、全格子点を未知数とする連立方程式を解くことで解が得られるが、格子点数が極めて多いと、係数行列が大きくなり、計算機メモリに納まらなくなる。 そのため、連立線形方程式の反復解法が利用される。

連立線形方程式の反復解法として、次のものがよく利用される。

先頭に戻る

SOR法

緩和法やSOR法では、すべての未知数の初期値を仮定し、基礎式(28)を変形し、目的関数 \( O_{i,j} \) を求める。 初期値を仮定しているため、目的関数はゼロにはならない。ここで格子点(i,j)の正の x方向の隣の格子点を E (East) 、負のx方向の隣の格子点を W(West)、同様に正のy方向の格子点をN (North)、負のy方向の格子点を S(South)と添字で表す。また中央(i,j)の格子点をC (Center)とした。 また各項の係数を \( c_x, x=NEWS \)とした。 \[ \begin{align*} O_C \equiv c_W T_W + c_C T_C + c_E T_E + c_S T_S + c_C T_C + c_N T_N - f_C = 0 \tag{29} \\ \end{align*} \]

(29)式を、ゼロとするよう修正幅 \( \Delta T_C \)は、一変数のNewton法を用い、次のように求められる。 \[ \begin{align*} \Delta T_C = - \frac {O_C}{c_C} \tag{30} \\ \end{align*} \]

従って、(30)式に緩和係数ωを考慮し、次のトライアルn+1回目の値として次式で更新すればよい。 \[ \begin{align*} T_C^{n+1}=T_C^n - \omega \frac {O_C}{c_C} \tag{31} \\ \end{align*} \]

通常の緩和法ではω=1.0を使うが、SOR法では過緩和 1 < ω < 2が採用される。緩和係数は収束を加速するパラメータである。 SOR法では、格子点を一つづつ解いており、点緩和とも呼ばれる。

なお、収束判定は残渣である目的関数 \( O_{i,j} \)の標準偏差を計算し、これが判定条件より小さくなれば収束したとみなす。

先頭に戻る

LSOR法

LSOR法（線緩和）は、y方向の値 NorthとSouthの値を固定し、 図７で x方向の格子点（分割数をNとすると内部の格子点N-1個）だけを連立して、(N-1)元の連立方程式として、一行全部を同時に解く方法である。 そして、y方向に繰り返し線緩和で順番に解き、すべての格子点がゼロとなるまで反復する。

一行だけを未知数とすることで、連立方程式の係数行列は三行対角行列（tridiagonal matrix、バンド行列）となり、計算機メモリの節約、計算速度の向上が、点緩和より促進できる。

先頭に戻る

ADI法

ADI法は、LSOR法を x方向および y方向を交互に解く方法である。 (29)式のNEWS添字を利用すると、ADI法はまず第１ステップとして、x方向の式(32)の三行対角行列を解き、中間ステップの解 \( T_x^* \)を得ます。これをすべての x方向に掃引します。 次に第２ステップとして、y方向の式(33)の三行対角行列をとき、n+1回目の値 \( T_y^{n+1} \)を解きます。同じくすべての y方向に掃引します。 これを残渣がゼロになるまで繰り返します。 \[ \begin{align*} c_E T_E^* + \omega c_C T_C^* + c_W T_W^* & = f_C - c_S T_S^n -(1-\omega)c_C T_C^n - c_N T_N^n \tag{32} \\ c_S T_S^{n+1} + \omega c_C T_C^{n+1} + c_N T_N^{n+1} & = f_C - c_W T_W^* -(1-\omega)c_C T_C^* - c_E T_E^* \tag{33} \\ \end{align*} \]

ここでωの値は、1 < ω < 2の値をとる。

演習問題２：Laplace方程式の解法

図７のような二次元平面を考える。x=0,x=1およびy=0,y=1に壁面を考える。囲まれた正方形の領域内の定常の二次元熱伝導問題は、次のLaplace式で与えられる。 \[ \begin{align} \frac{\partial^2 T}{\partial x^2} + \frac {\partial ^2 T}{\partial y^2} & = 0 \tag{A7} \\ {\rm BC1:} \quad T(0,y) & = 0 \\ {\rm BC2:} \quad T(1,y) & = 1 \\ {\rm BC3:} \quad T(x,0) & = 0 \\ {\rm BC4:} \quad T(x,1) & = 0 \\ \end{align} \]

x方向およびy方向を20等分し、内点の初期値として0.0を用い、SOR法で解くコードを作成しなさい。 そして緩和係数を変えて、収束性を比較しなさい。

演習問題３：Laplace方程式の解法

演習問題２を、LSOR法、ADI法で解き、収束性をSOR法と比較しなさい。

Poissonの方程式は、圧縮性流体の流体解析（CFD）時に圧力のPoisson方程式として出現する。また境界適合格子を自動生成するときにも、基礎方程式はPoisson方程式が現れる。 差分法や有限要素法ではよく現れ、解法をツール化しておくと便利。

先頭に戻る

演習問題の解答

上の演習問題の解答、および関連ファイルのダウンロードは、こちら（未リンク）で取り扱っています。

先頭に戻る

Literature Cited

先頭に戻る